【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴负半轴上,且满足S△COD=![]() S△BOC,求点D的坐标.
S△BOC,求点D的坐标.

参考答案:
【答案】(1)k=-1,b=4;(2)点D的坐标为(0,-4).
【解析】
(1)利用一次函数图象上点的坐标特征可求出点C的坐标,根据点A、C的坐标,利用待定系数法即可求出k、b的值;
(2)利用一次函数图象上点的坐标特征可求出点B的坐标,设点D的坐标为(0,m)(m<0),根据三角形的面积公式结合S△COD=![]() S△BOC,即可得出关于m的一元一次方程,解之即可得出m的值,进而可得出点D的坐标.
S△BOC,即可得出关于m的一元一次方程,解之即可得出m的值,进而可得出点D的坐标.
(1)当x=1时,y=3x=3,
∴点C的坐标为(1,3).
将A(﹣2,6)、C(1,3)代入y=kx+b,
得:![]() ,
,
解得:![]() .
.
(2)当y=0时,有﹣x+4=0,
解得:x=4,
∴点B的坐标为(4,0).
设点D的坐标为(0,m)(m<0),
∵S△COD=![]() S△BOC,即﹣
S△BOC,即﹣![]() m=
m=![]() ×
×![]() ×4×3,
×4×3,
解得:m=-4,
∴点D的坐标为(0,-4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P与点Q都在y轴上,且关于x轴对称.
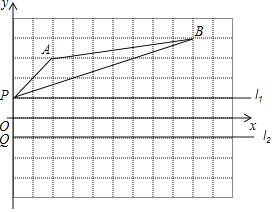
(1)请画出△ABP关于x轴的对称图形△A′B′Q(其中点A的对称点用A′表示,点B的对称点用B′表示);
(2)点P、Q同时都从y轴上的位置出发,分别沿l1、l2方向,以相同的速度向右运动,在运动过程中是否在某个位置使得AP+BQ=A′B成立?若存在,请你在图中画出此时PQ的位置(用线段P′Q′表示),若不存在,请你说明理由(注:画图时,先用铅笔画好,再用钢笔描黑).
-
科目: 来源: 题型:
查看答案和解析>>【题目】“国庆”期间,某电影院装修后重新开业,试营业期间统计发现,影院每天售出的电影票张数y(张)与电影票售价
 (元/张)之间满足一次函数关系:
(元/张)之间满足一次函数关系:  ,
, 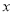 是整数,影院每天运营成本为1600元,设影院每天的利润为w(元)(利润=票房收入
是整数,影院每天运营成本为1600元,设影院每天的利润为w(元)(利润=票房收入 运营成本).
运营成本).(1)试求w与
 之间的函数关系式;
之间的函数关系式; (2)影院将电影票售价定为多少时,每天获利最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划购买20张课桌和一批椅子,该校了解到甲、乙两家商场以同样的价格出售同一型号的课桌与椅子,课桌报价200元/张,椅子报价50元/把.甲、乙两商场分别给出了不同的优惠方案.甲商场的优惠方案:凡买一张课桌赠送一把椅子;乙商场的优惠方案:所有课桌和椅子均按报价的九折销售.若该校需要
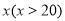 把椅子,在甲商场购买所花费用为
把椅子,在甲商场购买所花费用为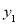 (元),在乙商场购买所花总费用为
(元),在乙商场购买所花总费用为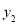 (元).
(元).(1)请分别写出
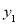 ,
,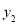 与
与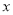 之间的函数关系式;
之间的函数关系式;(2)该校计划用8100元购买课桌和椅子,选甲、乙哪一家商场可以购买到尽可能多的椅子,说明理由;
(3)该校选择甲、乙哪一家商场花费较少?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知:AB∥CD,点E,F分别在AB,CD上,且OE⊥OF.
(1)求证:∠1+∠2=90°;
(2)如图2,分别在OE,CD上取点G,H,使FO平分∠CFG,EO平分∠AEH,求证:FG∥EH.
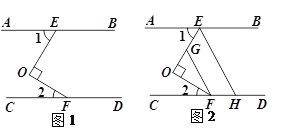
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC 中,AB=AC,D 是直线 BC 上一点(不与点 B、C 重合),以 AD 为一边在 AD的右侧作△ADE,AD=AE,∠DAE=∠BAC,连接 CE.
(1)如图 1,当点 D 在线段 BC 上时,求证:△ABD≌△ACE;
(2)如图 2,当点 D 在线段 BC 上时,如果∠BAC=90°,求∠BCE 的度数;
(3)如图 3,若∠BAC=α,∠BCE=β.点 D 在线段 CB 的延长线上时,则α、β之间有怎样 的数量关系?并证明你的结论.



相关试题

