【题目】数学课上,王老师布置如下任务:如图,△ABC中,BC>AB>AC,在BC边上取一点P,使∠APC=2∠ABC.

小路的作法如下:
① 作AB边的垂直平分线,交BC于点P,交AB于点Q;
② 连结AP.
请你根据小路同学的作图方法,利用直尺和圆规完成作图(保留作图痕迹);并完成以下推理,注明其中蕴含的数学依据:
∵ PQ是AB的垂直平分线
∴ AP= , (依据: );
∴ ∠ABC= , (依据: ).
∴ ∠APC=2∠ABC.
参考答案:
【答案】尺规作图见解析;BP,线段垂直平分线上的点到线段两个端点的距离相等;∠BAP,等边对等角.
【解析】
按照线段垂直平分线的作图方法作出AB的垂直平分线,然后按照线段垂直平分线的性质、等腰三角形的性质、三角形外角的性质求解即可.
如图,

∵ PQ是AB的垂直平分线
∴ AP=BP,(依据:线段垂直平分线上的点到线段两个端点的距离相等);
∴ ∠ABC=∠BAP,(依据:等边对等角).
∴ ∠APC=2∠ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=130°,∠COD=80°,OM,ON分别是∠AOB和∠COD的平分线.
(1)如果OA,OC重合,且OD在∠AOB的内部,如图1,求∠MON的度数;
(2)如果将图1中的∠COD绕点O点顺时针旋转n°(0<n<155),如图2,
①∠MON与旋转度数n°有怎样的数量关系?说明理由;
②当n为多少时,∠MON为直角?
(3)如果∠AOB的位置和大小不变,∠COD的边OD的位置不变,改变∠COD的大小;将图1中的OC绕着O点顺时针旋转m°(0<m<100),如图3,∠MON与旋转度数m°有怎样的数量关系?说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的切线,B为切点,AO的延长线交⊙O于点C,连接BC,如果∠A=30°,AB=2
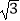 ,那么AC的长等于( )
,那么AC的长等于( )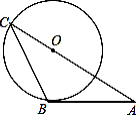
A.4
B.6
C.4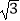
D.6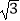
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,AD,BC是⊙O的两条互相垂直的直径,点P从点O出发沿图中某一个扇形顺时针匀速运动,设∠APB=y(单位:度),如果y与点P运动的时间x(单位:秒)的函数关系的图象大致如图2所示,那么点P的运动路线可能为( )
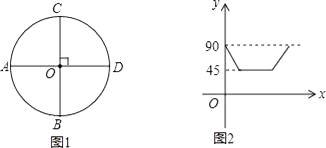
A.O→B→A→O
B.O→A→C→O
C.O→C→D→O
D.O→B→D→O -
科目: 来源: 题型:
查看答案和解析>>【题目】本学期学习了分式方程的解法,下面是晶晶同学的解题过程:
解方程

解:整理,得:
 …………………………第①步
…………………………第①步去分母,得:
 …………………………第②步
…………………………第②步移项,得:
 ……………………… 第③步
……………………… 第③步合并同类项,得:
 ……………………… 第④步
……………………… 第④步系数化1,得:
 …………………………第⑤步
…………………………第⑤步检验:当
 时,
时,
所以原方程的解是
 . ………………………第⑥步
. ………………………第⑥步上述晶晶的解题过程从第_____步开始出现错误,错误的原因是_________________.请你帮晶晶改正错误,写出完整的解题过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习相似三角形和解直角三角形的相关内容后,张老师请同学们交流这样的一个问题:“如上图,在正方形网格上有△A1B1C1和△A2B2C2 , 这两个三角形是否相似?”,那么你认为△A1B1C1和△A2B2C2 , (相似或不相似);理由是 .
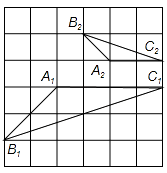
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明四等分弧AB,他的作法如下:
①连接AB(如图);作AB的垂直平分线CD交弧AB于点M,交AB于点T;
②分别作AT,TB的垂直平分线EF,GH,交弧AB于N,P两点,则N,M,P三点把弧AB四等分。你认为小明的作法是否正确: , 理由是。
相关试题

