【题目】已知∠AOB=130°,∠COD=80°,OM,ON分别是∠AOB和∠COD的平分线.
(1)如果OA,OC重合,且OD在∠AOB的内部,如图1,求∠MON的度数;
(2)如果将图1中的∠COD绕点O点顺时针旋转n°(0<n<155),如图2,
①∠MON与旋转度数n°有怎样的数量关系?说明理由;
②当n为多少时,∠MON为直角?
(3)如果∠AOB的位置和大小不变,∠COD的边OD的位置不变,改变∠COD的大小;将图1中的OC绕着O点顺时针旋转m°(0<m<100),如图3,∠MON与旋转度数m°有怎样的数量关系?说明理由.

参考答案:
【答案】(1)25°;(2)①n°+25°,②n=65°;(3)![]() m°+25°.
m°+25°.
【解析】
(1)如图1,根据OM平分∠AOB,∠AOB=130°,利用角平分线的定义可得:∠AOM=![]() ∠AOB=
∠AOB=![]() ×130°=65°,再根据ON平分∠COD,∠COD=80°,可得∠AON=
×130°=65°,再根据ON平分∠COD,∠COD=80°,可得∠AON=![]() ∠COD=
∠COD=![]() ×80°=40°,
×80°=40°,
进而求出∠MON=∠AOM﹣∠AON=65°﹣40°=25°,
(2)①如图2中,根据图形中角的和差关系可得:∠MON=∠COM﹣∠NOC=65°+n°﹣40°=n°+25°,
②当∠MON=90°时,由于n°+25°=90°,所以n=65°,
(3)如图3中,根据图中角的和差关系可得:∠MON=∠COM﹣∠CON=65°+m°﹣![]() (80°+m°)=
(80°+m°)=![]() m°+25°.
m°+25°.
(1)如图1,∵OM平分∠AOB,∠AOB=130°,
∴∠AOM=![]() ∠AOB=
∠AOB=![]() ×130°=65°,
×130°=65°,
∵ON平分∠COD,∠COD=80°,
∴∠AON=![]() ∠COD=
∠COD=![]() ×80°=40°,
×80°=40°,
∴∠MON=∠AOM﹣∠AON=65°﹣40°=25°,
(2)①如图2中,∠MON=∠COM﹣∠NOC=65°+n°﹣40°=n°+25°,
②当∠MON=90°时,n°+25°=90°,
∴n=65°,
(3)如图3中,∠MON=∠COM﹣∠CON=65°+m°﹣![]() (80°+m°)=
(80°+m°)=![]() m°+25°.
m°+25°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=2
 ,∠BAC=120°,点D、E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为_____.
,∠BAC=120°,点D、E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小芳在本学期的体育测试中,1分钟跳绳获得了满分,她的“满分秘籍”如下:前20秒由于体力好,小芳速度均匀增加,20秒至50秒保持跳绳速度不变,后10秒进行冲刺,速度再次均匀增加,最终获得满分,反映小芳1分钟内跳绳速度y(个/秒)与时间t(秒)关系的函数图象大致为( )

A. A B. B C. C D. D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x+3与y轴交于A点,与反比例函数y=
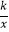 (x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0). 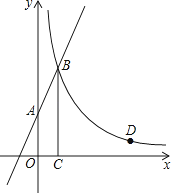
(1)求反比例函数的解析式;
(2)点D(a,1)是反比例函数y=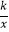 (x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店在甲批发市场以每包m元的价格进了40包茶叶,又在乙批发市场以每包n元(m>n)的价格进了同样的60包茶叶,如果商家以每包
 元的价格卖出这种茶叶,卖完后,这家商店( )
元的价格卖出这种茶叶,卖完后,这家商店( )A.盈利了 B.亏损了 C.不赢不亏 D.盈亏不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|a+b|+|a-b|-2b=0,在数轴上给出关于a,b的四种位置关系如图所示,则可能成立的有( )

A. 1种 B. 2种 C. 3种 D. 4种
-
科目: 来源: 题型:
查看答案和解析>>【题目】为确保信息安全,信息需要加密传输,其原理如下:

现将10个数字按图所示排成一个圈,并设置了一种数字信息的加密规则:加密钥匙为“n&3”,“n&3”代表“把明文n换成图中从它开始顺时针跳过3个数字的那个数字”,例如明文是5时,对应的密文为9.若收到的密文是6452,那么通过解密,它对应的明文是______.
相关试题

