【题目】现有甲、乙两个容器,分别装有进水管和出水管,两容器的进、出水速度不变,先打开乙容器的进水管,2分钟时再打开甲容器的进水管,又过2分钟关闭甲容器的进水管,再过4分钟同时打开甲容器的进、出水管.直到12分钟时,同时关闭两容器的进、出水管.打开和关闭水管的时间忽略不计.容器中的水量y(升)与乙容器注水时间x(分)之间的关系如图所示.
(1)求甲容器的进、出水速度;
(2)甲容器的进、出水管都关闭后,是否存在两容器的水量相等?若存在,求出此时的时间.

参考答案:
【答案】(1)甲容器的进水速度:![]() =5(升/分),甲容器的出水速度为5-
=5(升/分),甲容器的出水速度为5-![]() =3(升/分);(2)存在,理由见解析;(3)乙容器进水管打开8分钟时,两容器的水量相等
=3(升/分);(2)存在,理由见解析;(3)乙容器进水管打开8分钟时,两容器的水量相等
【解析】
(1)根据图示知,甲容器是在2分钟内进水量为10升;
(2) 利用待定系数法求得该函数解析式.
解:(1)甲容器的进水速度:![]() =5(升/分),甲容器的出水速度为5-
=5(升/分),甲容器的出水速度为5-![]() =3(升/分).
=3(升/分).
(2)存在.
甲容器的进、出水管都关闭是在第4分钟至第8分钟间,此时甲容器的水量为10升.由题意可知,甲容器在第3分钟时的水量为5×(3-2)=5(升),且此时,乙容器的水量也为5升.
设y乙=kx+b(k≠0),依题意得:3k+b=5,b=2,
解得k=1,b=2,
所以y乙=x+2.
当y乙=10时,x=8.
所以乙容器进水管打开8分钟时,两容器的水量相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:
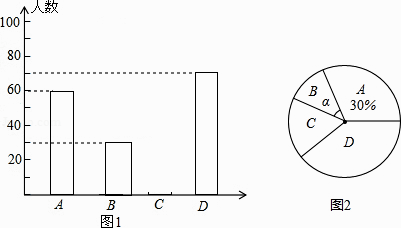
(1)本次抽样调查共抽取了多少名学生?并将条形统计图补充完整;
(2)本次抽样调查中,学习时间的中位数落在哪个等级内?
(3)表示B等级的扇形圆心角α的度数是多少?
(4)在此次问卷调查中,甲班有2人平均每天课外学习时间超过2小时,乙班有3人平均每天课外学习时间超过2小时,若从这5人中任选2人去参加座谈,试用列表或化树状图的方法求选出的2人来自不同班级的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x)
1
2
3
4
…
座位数(y)
50
53
56
59
…
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B在点A正南的方向上,与点A的距离为lcm;点C在点A北偏东30°的方向上,与点A的距离为2cm;点D在点A正西的方向上,与点A的距离为3cm.以点A为原点,正北方向为y轴,建立平面直角坐标系,规定一个单位长度代表1cm长.
(1)画出点C、D;
(2)写出点B、D的坐标,将点B作怎样的平移可得到点D?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,连结AF,CE.求证:四边形AECF是平行四边形.
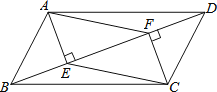
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家食品公司的市场调查员将本公司生产的一种新点心免费送给50人品尝,以调查这种点心的甜度是否适中.根据调查结果绘制了如下尙不完整的统计图;
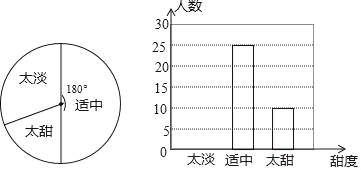
(1)求本次调查中,认为“甜度太甜”的人数占被调查总人数的百分比;
(2)求被调查的50人中,认为“甜度太淡”的人数;
(3)完成条形图;
(4)求扇形图中,“甜度太淡”对应扇形的圆心角度数.
相关试题

