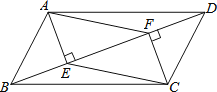
【题目】如图,在平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,连结AF,CE.求证:四边形AECF是平行四边形.
参考答案:
【答案】见解析
【解析】
试题分析:由四边形ABCD是平行四边形,可得AB=CD,AB∥CD,又由AE⊥BD,CF⊥BD,即可得AE∥CF,∠AEB=∠CFD=90°,然后利用AAS证得△AEB≌△CFD,即可得AE=CF,由有一组对边相等且平行的四边形是平行四边形,即可证得四边形AECF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴AE∥CF,∠AEB=∠CFD=90°,
在△AEB和△CFD中,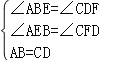 ,
,
∵∴△AEB≌△CFD(AAS),
∴AE=CF,
∴四边形AECF是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x)
1
2
3
4
…
座位数(y)
50
53
56
59
…
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有甲、乙两个容器,分别装有进水管和出水管,两容器的进、出水速度不变,先打开乙容器的进水管,2分钟时再打开甲容器的进水管,又过2分钟关闭甲容器的进水管,再过4分钟同时打开甲容器的进、出水管.直到12分钟时,同时关闭两容器的进、出水管.打开和关闭水管的时间忽略不计.容器中的水量y(升)与乙容器注水时间x(分)之间的关系如图所示.
(1)求甲容器的进、出水速度;
(2)甲容器的进、出水管都关闭后,是否存在两容器的水量相等?若存在,求出此时的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B在点A正南的方向上,与点A的距离为lcm;点C在点A北偏东30°的方向上,与点A的距离为2cm;点D在点A正西的方向上,与点A的距离为3cm.以点A为原点,正北方向为y轴,建立平面直角坐标系,规定一个单位长度代表1cm长.
(1)画出点C、D;
(2)写出点B、D的坐标,将点B作怎样的平移可得到点D?

-
科目: 来源: 题型:
查看答案和解析>>【题目】一家食品公司的市场调查员将本公司生产的一种新点心免费送给50人品尝,以调查这种点心的甜度是否适中.根据调查结果绘制了如下尙不完整的统计图;
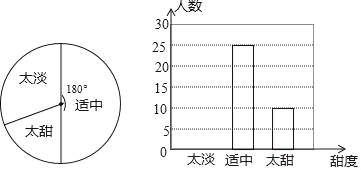
(1)求本次调查中,认为“甜度太甜”的人数占被调查总人数的百分比;
(2)求被调查的50人中,认为“甜度太淡”的人数;
(3)完成条形图;
(4)求扇形图中,“甜度太淡”对应扇形的圆心角度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】市政府要求武汉轻轨二七路段工程12个月完工。现由甲、乙两工程队参与施工,已知甲队单独完成需要16个月,每月需费用600万元;乙队单独完成需要24个月,每月需费用400万元。由于前期工程路面较宽,可由甲、乙两队共同施工。随着工程的进行,路面变窄,两队再同时施工,对交通影响较大,为了减小对解放大道的交通秩序的影响,后期只能由一个工程队施工.工程总指挥部结合实际情况现拟定两套工程方案:
①先由甲、乙两个工程队合做m个月后,再由甲队单独施工,保证恰好按时完成.
②先由甲、乙两个工程队合做n个月后,再由乙队单独施工,也保证恰好按时完成.
⑴求两套方案中m和n的值;
⑵通过计算,并结合施工费用及施工对交通的影响,你认为该工程总指挥部应该选择哪种方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(
 ,1)在反比例函数y=
,1)在反比例函数y=  的图象上.
的图象上.
(1)求反比例函数y= 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP= S△AOB , 求点P的坐标;
S△AOB , 求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上.
相关试题

