【题目】下列各数中,数值相等的有( )
(1)32和23;(2)-23与(-2)3;(3)22与(-2)2;(4)-22与(-2)2;(5)-32与(-3)2;(6)![]() 与
与![]() ;(7)(-1)11与-1;(8)-(-0.1)3与0.001.
;(7)(-1)11与-1;(8)-(-0.1)3与0.001.
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】D
【解析】
直接利用有理数的乘方运算法则计算得出答案.
(1)32=9,23=8,故(1)中两数值不相等;
(2)-23=-8,(-2)3=-8,故(2)中两数值相等;
(3)22=4,(-2)2=4,故(3)中两数值相等;
(4)-22=-4,(-2)2=4,故(4)中两数值不相等;
(5)-32=-9,(-3)2=9,故(5)中两数值不相等;
(6)![]() =
=![]() ≠
≠![]() ,故(6)中两数值不相等;
,故(6)中两数值不相等;
(7)(-1)11=-1,故(7)中两数值相等;
(8)-(-0.1)3=0.001,故(8)中两数值相等.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点C在线段AB上,AC = 8 cm,CB = 6 cm,点M、N分别是AC、BC的中点.

(1)求线段MN的长.
(2)若C为线段AB上任意一点,满足AC+CB=a(cm),其他条件不变,你能猜想出MN的长度吗?并说明理由.
(3)若C在线段AB的延长线上,且满足AC-CB=b(cm),M、N分别为AC、BC的中点,你能猜想出MN的长度吗?请画出图形,写出你的结论,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,BC⊥AB于点B,连接OC交⊙O于点E,弦AD∥OC,弦DF⊥AB于点G.
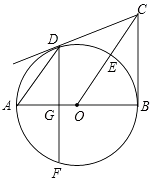
(1)求证:点E是 的中点;
的中点;
(2)求证:CD是⊙O的切线;
(3)若AD=12,⊙O的半径为10,求弦DF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:直线AB经过点A(0,3)点B(
 ,0),点M在y轴上,⊙M经过点A、B,交x轴于另一点C.
,0),点M在y轴上,⊙M经过点A、B,交x轴于另一点C. 
(1)求直线AB的解析式;
(2)求点M的坐标;
(3)点P是劣弧AC上一个动点,当P点运动时,问:线段PA,PB,PC有什么数量关系?并给出证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将一张长方形的纸片连续对折,对折时每次折痕与上次的折痕保持平行,对折一次得到1条折痕(图中虚线),对折二次得到3条折痕,对折三次得到7条折痕,那么对折2018次后可以得到________条折痕.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,函数y=ax2+bx+c(a>0)的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),OB=OC,OC=3OA.

(1)求这个二次函数的表达式;
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,下列说法:①∠APE=∠C,② AQ=BQ,③BP=2PQ, ④AE+BD=AB,其正确的个数有( )个.

A. 1 B. 2 C. 3 D. 4
相关试题

