【题目】如图:直线AB经过点A(0,3)点B( ![]() ,0),点M在y轴上,⊙M经过点A、B,交x轴于另一点C.
,0),点M在y轴上,⊙M经过点A、B,交x轴于另一点C. 
(1)求直线AB的解析式;
(2)求点M的坐标;
(3)点P是劣弧AC上一个动点,当P点运动时,问:线段PA,PB,PC有什么数量关系?并给出证明.
参考答案:
【答案】
(1)解:设直线AB的解析式为y=kx+b,
把点A(0,3)和点B( ![]() ,0)代入y+kx+b得到
,0)代入y+kx+b得到 ![]() ,
,
解得 ![]() ,
,
∴直线AB的解析式为y=﹣ ![]() x+3
x+3
(2)解:如图1中,连接BM.设AM=BM=r.
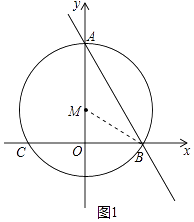
在Rt△BMO中,
∵OM2+OB2=BM2,OM=3﹣r,OB= ![]() ,
,
∴(3﹣r)2+( ![]() )2=r2,
)2=r2,
∴r=2,
∴OM=3﹣2=1,
∴点M坐标为(0,1)
(3)解:结论:PB=PA+PC,理由如下:
如图2中,连接AC、在PB上截取PN=PC,连接CN.
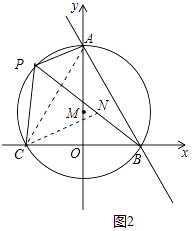
∵OM⊥BC,
∴OC=OB,
∴AC=AB,
∵tan∠ABO= ![]() =
= ![]() =
= ![]() ,
,
∴∠ABC=60°,
∴△ABC是等边三角形,
∴AC=CB,∠ACB=∠CAB=60°,
∴∠CPB=∠CAB=60°,∵PC=PN,
∴△PCN是等边三角形,
∴CP=CN,∠PCN=60°,
∴∠PCN=∠ACB=60°,
∴∠PCA=∠NCB,∵PC=CN,CA=CB,
∴△PCA≌△NCB,
∴PA=BN,
∵PB=PN+BN,PN=PC,BN=PA,
∴PB=PA+PC.
【解析】(1)设直线AB的解析式为y=kx+b,把点A(0,3)和点B( ![]() ,0)代入y+kx+b得到
,0)代入y+kx+b得到 ![]() 解方程组即可.(2)如图1中,连接BM.设AM=BM=r.在Rt△BMO中,由OM2+OB2=BM2 , OM=3﹣r,OB=
解方程组即可.(2)如图1中,连接BM.设AM=BM=r.在Rt△BMO中,由OM2+OB2=BM2 , OM=3﹣r,OB= ![]() ,可得(3﹣r)2+(
,可得(3﹣r)2+( ![]() )2=r2 , 解方程即可.(3)结论:PB=PA+PC,如图2中,连接AC、在PB上截取PN=PC,连接CN.首先证明△ACB,△PCN都是等边三角形,再证明△PCA≌△NCB,推出PA=BN,由此即可解决问题.
)2=r2 , 解方程即可.(3)结论:PB=PA+PC,如图2中,连接AC、在PB上截取PN=PC,连接CN.首先证明△ACB,△PCN都是等边三角形,再证明△PCA≌△NCB,推出PA=BN,由此即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABO的三个顶点的坐标分别为O(0,0),A(5,0),B(2,4).
(1)求△OAB的面积;
(2)若O,A两点的位置不变,P点在什么位置时,△OAP的面积是△OAB面积的2倍?
(3)若B(2,4),O(0,0)不变,M点在x轴上,M点在什么位置时,△OBM的面积是△OAB面积的2倍?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点C在线段AB上,AC = 8 cm,CB = 6 cm,点M、N分别是AC、BC的中点.

(1)求线段MN的长.
(2)若C为线段AB上任意一点,满足AC+CB=a(cm),其他条件不变,你能猜想出MN的长度吗?并说明理由.
(3)若C在线段AB的延长线上,且满足AC-CB=b(cm),M、N分别为AC、BC的中点,你能猜想出MN的长度吗?请画出图形,写出你的结论,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,BC⊥AB于点B,连接OC交⊙O于点E,弦AD∥OC,弦DF⊥AB于点G.
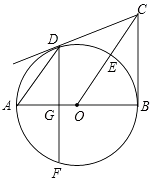
(1)求证:点E是 的中点;
的中点;
(2)求证:CD是⊙O的切线;
(3)若AD=12,⊙O的半径为10,求弦DF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数中,数值相等的有( )
(1)32和23;(2)-23与(-2)3;(3)22与(-2)2;(4)-22与(-2)2;(5)-32与(-3)2;(6)
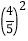 与
与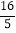 ;(7)(-1)11与-1;(8)-(-0.1)3与0.001.
;(7)(-1)11与-1;(8)-(-0.1)3与0.001.A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将一张长方形的纸片连续对折,对折时每次折痕与上次的折痕保持平行,对折一次得到1条折痕(图中虚线),对折二次得到3条折痕,对折三次得到7条折痕,那么对折2018次后可以得到________条折痕.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,函数y=ax2+bx+c(a>0)的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),OB=OC,OC=3OA.

(1)求这个二次函数的表达式;
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度.
相关试题

