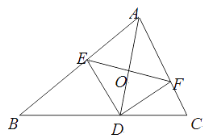
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④ AE2+DF2=AF2+DE2.上述结论中正确的是( )
A. ②③ B. ②④ C. ①②③ D. ②③④
参考答案:
【答案】D
【解析】
由AD是角平分线及DE、DF均为高可知△AED≌△AFD,则可得AE=AF,DE=DF,继而得到AD是EF的垂直平分线,由此可判断②和③正误,再由勾股定理可判断④的正误,而①的结论无法由已知条件推出.
解:∵AD是角平分线,
∴∠EAD=∠FAD,
∵∠AED=∠AFD=90°,AD=AD,
∴△ADE≌△AFD,
∴AE=AF,DE=DF,
∴AD⊥EF,②正确,
∵∠BAC=90°,∠AED=∠AFD=90°
又∵AE=AF,
∴四边形AEDF是正方形,③正确,
∵∠AED=∠AFD=90°,
∴AE2+DE2=AF2+DF2=AD2
∵DE=DF,
∴AE2+DF2=AF2+DE2,④正确.
根据前述已得结论,需要四边形AEDF是菱形才能得到OA=OD的结论,而题干并未给出这个条件,①错误,
故选择D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,斜边AB=5,而直角边BC,AC之长是一元二次方程x2-(2m-1)x+4(m-1)=0的两根,则m的值是( )
A. 4 B. -1 C. 4或-1 D. -4或1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是

A. AB=
 EF B. AB=2EF C. AB=
EF B. AB=2EF C. AB= EF D. AB=
EF D. AB=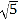 EF
EF -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,CE=BD,求证:△ADE为等边三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】按指定的方法解下列方程:
(1)2x2-5x-4=0(配方法);
(2)3(x-2)+x2-2x=0(因式分解法);
(3)(a2-b2)x2-4abx=a2-b2(a2≠b2)(公式法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料,解答问题:为解方(x2﹣1)2﹣5(x2﹣1)+6=0.我们可以将(x2﹣1)看作一个整体,然后x2﹣1=y,那么原方程可化为y2﹣5y+6=0,解得y1=2,y2=3.
当y=2时,x2﹣1=2,x2=3,x=±
 ;
;当y=3时,x2﹣1=3,x2=4,x=±2.
当原方程的解为x1=
 , x2=﹣
, x2=﹣ , x3=2,x4=﹣2.
, x3=2,x4=﹣2.上述解题方法叫做“换元法”;请利用“换元法”解方程.(x2+x)2﹣4(x2+x)﹣12=0.
相关试题

