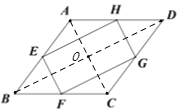
【题目】如图,在菱形ABCD中,点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是

A. AB=![]() EF B. AB=2EF C. AB=
EF B. AB=2EF C. AB=![]() EF D. AB=
EF D. AB=![]() EF
EF
参考答案:
【答案】D
【解析】连接AC、BD交于点O,由菱形的性质可得OA=![]() AC,OB=
AC,OB=![]() BD,AC⊥BD,由中位线定理可得EH=
BD,AC⊥BD,由中位线定理可得EH=![]() BD,EF=
BD,EF=![]() AC,根据EH=2EF,可得OA=EF,OB=2EF,在Rt△AOB中,根据勾股定理即可求得AB=
AC,根据EH=2EF,可得OA=EF,OB=2EF,在Rt△AOB中,根据勾股定理即可求得AB=![]() EF,由此即可得到答案.
EF,由此即可得到答案.
连接AC、BD交于点O,
∵四边形ABCD是菱形,∴OA=![]() AC,OB=
AC,OB=![]() BD,AC⊥BD,
BD,AC⊥BD,
∵E、F、G、H分别是边AB、BC、CD和DA的中点,
∴EH=![]() BD,EF=
BD,EF=![]() AC,
AC,
∵EH=2EF,
∴OA=EF,OB=2OA=2EF,
在Rt△AOB中,AB=![]() =
=![]() EF,
EF,
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分)在长方形ABCD中,AB=5cm,BC=6cm,点P从点A开始沿边AB向终点B以1cm/s的速度移动,与此同时,点Q从点C开始沿边CB向终点B以2cm/s的速度移动,如果P、Q分别从A、C同时出发,当点Q运动到点B时,两点停止运动.设运动时间为t秒.

(1)填空:BQ=______________cm,PB=_______________cm(用含t的代数式表示);
(2)当t为何值时,PQ的长度等于
 cm?
cm?(3)是否存在t的值,使得五边形APQCD的面积等于27
 ?若存在,请求出此时t的值;若不存在,请说明理由
?若存在,请求出此时t的值;若不存在,请说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图, △ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC
⑴求∠ECD的度数;
⑵若CE=5,求CB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,斜边AB=5,而直角边BC,AC之长是一元二次方程x2-(2m-1)x+4(m-1)=0的两根,则m的值是( )
A. 4 B. -1 C. 4或-1 D. -4或1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,CE=BD,求证:△ADE为等边三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④ AE2+DF2=AF2+DE2.上述结论中正确的是( )
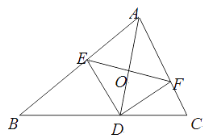
A. ②③ B. ②④ C. ①②③ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是 .

相关试题

