【题目】按指定的方法解下列方程:
(1)2x2-5x-4=0(配方法);
(2)3(x-2)+x2-2x=0(因式分解法);
(3)(a2-b2)x2-4abx=a2-b2(a2≠b2)(公式法).
参考答案:
【答案】(1)x1=![]() ,x2=
,x2=![]() ;(2)x1=2,x2=-3;(3)x1=
;(2)x1=2,x2=-3;(3)x1=![]() ,x2=-
,x2=-![]() .
.
【解析】
(1)根据用配方法解一元二次方程的步骤:移常数项到方程的右边、将二次项的系数化为1,再将方程的左边配方(方程两边同时加上一次项系数一般的平方),然后利用直接开平方法求解.(2)观察方程的特点:右边为0,左边可以分解因式,因此利用因式分解法解方程即可.(3)观察方程的特点,利用一元二次方程的求根公式法解此方程.
(1)∵2x2-5x-4=0,∴2x2-5x=4,
∴x2- ![]() x=2,
x=2,
∴x2- ![]() x+
x+ ![]() =2+
=2+ ![]() ,
,
∴(x- ![]() )2=
)2= ![]() ,
,
解得:x1= ![]() ,x2=
,x2= ![]() ;
;
(2)∵3(x-2)+x2-2x=0,∴3(x-2)+x(x-2)=0,
∴(x-2)(3+x)=0,
即x-2=0或3+x=0,
解得:x1=2,x2=-3;
(3)∵(a2-b2)x2-4abx=a2-b2(a2≠b2),∴(a2-b2)x2-4abx-(a2-b2)=0,
∴a=a2-b2 , b=-4ab,c=-(a2-b2)=b2-a2 ,
∴△=b2-4ac=(-4ab)2-4×(a2-b2)(b2-a2)=4(a2+b2)2 ,
∴x= ![]() ,
,
解得:x1= ![]() =
= ![]() ,x2=-
,x2=- ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,CE=BD,求证:△ADE为等边三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④ AE2+DF2=AF2+DE2.上述结论中正确的是( )
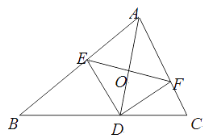
A. ②③ B. ②④ C. ①②③ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料,解答问题:为解方(x2﹣1)2﹣5(x2﹣1)+6=0.我们可以将(x2﹣1)看作一个整体,然后x2﹣1=y,那么原方程可化为y2﹣5y+6=0,解得y1=2,y2=3.
当y=2时,x2﹣1=2,x2=3,x=±
 ;
;当y=3时,x2﹣1=3,x2=4,x=±2.
当原方程的解为x1=
 , x2=﹣
, x2=﹣ , x3=2,x4=﹣2.
, x3=2,x4=﹣2.上述解题方法叫做“换元法”;请利用“换元法”解方程.(x2+x)2﹣4(x2+x)﹣12=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证:ABCD是菱形;
(2)若AB=5,AC=6,求ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形的一个角与三角形的一个角重合,然后它的对角顶点在这个重合角的对边上,这个菱形称为这个三角形的亲密菱形,如图,在△CFE中,CF=6,CE=12,∠FCE=45°,以点C为圆心,以任意长为半径作AD,再分别以点A和点D为圆心,大于
 AD长为半径做弧,交EF于点B,AB∥CD.
AD长为半径做弧,交EF于点B,AB∥CD.
(1)求证:四边形ACDB为△CFE的亲密菱形;
(2)求四边形ACDB的面积.
相关试题

