【题目】如图,已知抛物线y=x2+bx与x轴交于O,A(4,0)两点,点B的坐标为(0,-3).
(1)求抛物线的对称轴;
(2)已知点P在抛物线的对称轴上,连接OP,BP. 若要使OP+BP的值最小,求出点P的坐标;
(3)将抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象. 当直线y=x+m(m≠0)与这个新图象有两个公共点时,在反比例函数y=![]() 的图象中,y的值随x怎样变化?判断并说明理由.
的图象中,y的值随x怎样变化?判断并说明理由.

参考答案:
【答案】(1)抛物线的对称轴为直线x=2;(2)点P的坐标为(2,-![]() );
);
(3)y的值随x的增大而增大.
【解析】分析:(1)把点A(4,0)代入y=x2+bx,求出b,在利用![]() ,即可求解.(2) 作O点关于直线x=2对称的点,而P在直线x=2上,则利用轴对称最短路径即可求解;(3)由翻转的性质,再利用根的判别式和反比例函数的性质可判断出y随x的增大而减小。
,即可求解.(2) 作O点关于直线x=2对称的点,而P在直线x=2上,则利用轴对称最短路径即可求解;(3)由翻转的性质,再利用根的判别式和反比例函数的性质可判断出y随x的增大而减小。
本题解析:
(1)由题意得: ![]() ∴b=-4, ∴函数关系式为;y=x-4x, ∴对称轴为:
∴b=-4, ∴函数关系式为;y=x-4x, ∴对称轴为: ![]() ;
;
(2)由题意得:OP+PB的值最小,实际就是在同一直线一旁有两点,在直线上求点只要取O点关于直线x=2对称的点A(4,0),过AB的直线与直线x=2的交点就是点p,
设过AB的直线为y=kx-3,由B(4,0)在y=kx-3上,∴0=4k-3,得k=![]() ,
,![]() ,
,
∵P在直线x=2上,∴y=![]() ,∴P(2,-
,∴P(2,- ![]() ),
),
(3)∵y=x-4x在x轴下方的部分沿x轴翻转,
当直线y=x+m(m≠0)有两个不相同的解,∴△>0,3-4×m>0,得m<![]() ,又m>0, ∴0<m<
,又m>0, ∴0<m<![]() ,在反比例函数y=
,在反比例函数y=![]() 中,∵0<m=k<
中,∵0<m=k<![]() ,y随x的增大而减小.
,y随x的增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=12cm,BC=16cm,连接AC. 点P从点A出发,沿AB以1cm/s的速度向点B匀速运动,同时,直线l从点C出发,沿CA以1cm/s的速度向点A匀速运动,直线l分别交BC,CD于点E,F,且EF⊥AC,垂足为G,当点P停止运动时,直线l也停止运动,连接PF.设点P的运动时间为t(s)(0<t<12).
(1)当t为何值时,四边形PBCF是矩形?
(2)设四边形PBEF的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形PBEF ∶ S矩形ABCD=181∶384若存在,求出t的值;若不存在,请说明理由. (提示:1722=29584)

-
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个解为x≥1的一元一次不等式 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:△ABC和△ADE是等边三角形,AD是BC边上的中线.求证:BE=BD.

-
科目: 来源: 题型:
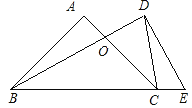
查看答案和解析>>【题目】将一副直角三角板如图摆放,等腰直角三角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同,且斜边BC与BE在同一直线上,AC与BD交于点O,连接CD.
求证:△CDO是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把代数式2x2﹣18分解因式,结果正确的是( )
A.2(x2﹣9)
B.2(x﹣3)2
C.2(x+3)(x﹣3)
D.2(x+9)(x﹣9) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,AC=BC,AC⊥BC于点C,过点C作直线EF∥AB,点D在直线EF上,连接BD,过点D作GD⊥BD,交直线AC于点H,连接BG.
(1)如图1所示,当点D在射线CF上,点H在射线AC上时,连接BH,过点D作MD⊥CD,交CB的延长线于点M. 求证:∠GBH+∠G=∠M;
(2)如图2所示,当点D在射线CE上,点H在射线CA上时,试判断并证明DH与BD之间的数量关系.


图1 图2
相关试题

