【题目】如图,在矩形ABCD中,AB=12cm,BC=16cm,连接AC. 点P从点A出发,沿AB以1cm/s的速度向点B匀速运动,同时,直线l从点C出发,沿CA以1cm/s的速度向点A匀速运动,直线l分别交BC,CD于点E,F,且EF⊥AC,垂足为G,当点P停止运动时,直线l也停止运动,连接PF.设点P的运动时间为t(s)(0<t<12).
(1)当t为何值时,四边形PBCF是矩形?
(2)设四边形PBEF的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形PBEF ∶ S矩形ABCD=181∶384若存在,求出t的值;若不存在,请说明理由. (提示:1722=29584)

参考答案:
【答案】(1)当t=![]() 时,四边形PBCF是矩形; (2)y=-
时,四边形PBCF是矩形; (2)y=-![]() t2+
t2+![]() t+96;(3)存在,t=6.
t+96;(3)存在,t=6.
【解析】分析:(1)由△FGC∽△CBA,得出CF=![]() t,再由CF=BP,即可求解;(2)由四边形PBEF的面积=S四边形PBCF-S△FEC, 代入求出y与t之间的函数关系式,可得出结论;(3)先计算矩形ABCD的面积,再将(2)得到的式子y代入到式子S四边形PBEF ∶ S矩形ABCD=181∶384中,解出即可.
t,再由CF=BP,即可求解;(2)由四边形PBEF的面积=S四边形PBCF-S△FEC, 代入求出y与t之间的函数关系式,可得出结论;(3)先计算矩形ABCD的面积,再将(2)得到的式子y代入到式子S四边形PBEF ∶ S矩形ABCD=181∶384中,解出即可.
本题解析:(1)易得△FGC∽△CBA,∴CF=![]() t. 当CF=BP时,四边形PBCF是矩形 (2)y=-
t. 当CF=BP时,四边形PBCF是矩形 (2)y=-![]() t2+
t2+![]() t+96;:y=S四边形PBCF-S△FEC(3)存在,t=6. -
t+96;:y=S四边形PBCF-S△FEC(3)存在,t=6. -![]() t2+
t2+![]() t+96=
t+96=![]() ×192,解得t=6
×192,解得t=6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知不等式
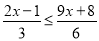 .
.(1)求该不等式的解集;
(2)该不等式的所有负整数解的和是关于y的方程2y-3a=6的解,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一段圆柱体的树干的示意图,已知树干的半径r=10cm,AD=45cm. (π值取3)
(1)若螳螂在点A处,蝉在点C处,图1中画出了螳螂捕蝉的两条路线,即A→D→C和A→C,图2是该圆柱体的侧面展开图,判断哪条路的距离较短,并说明理由;
(2)若螳螂在点A处,蝉在点D处,螳螂想要捕到这只蝉,但又怕蝉发现,于是螳螂绕到
后方去捕捉它,如图3所示,求螳螂爬行的最短距离;(提示:
 =75)
=75)(3)图4是该圆柱体的侧面展开图,蝉N在半径为10cm的⊙O的圆上运动,⊙O与BC相切,点O到CD的距离为20cm,螳螂M在线段AD运动上,连接MN,MN即为螳螂捕蝉时螳螂爬行的距离,若要使MN与⊙O总是相切,求MN的长度范围.

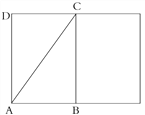


图1 图2 图3 图4
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下列各组线段的长为边,能组成三角形的是( )
A.3cm,6cm,8cmB.3cm,2cm,6cmC.5cm,6cm,11cmD.2cm,7cm,4cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个解为x≥1的一元一次不等式 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:△ABC和△ADE是等边三角形,AD是BC边上的中线.求证:BE=BD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2+bx与x轴交于O,A(4,0)两点,点B的坐标为(0,-3).
(1)求抛物线的对称轴;
(2)已知点P在抛物线的对称轴上,连接OP,BP. 若要使OP+BP的值最小,求出点P的坐标;
(3)将抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象. 当直线y=x+m(m≠0)与这个新图象有两个公共点时,在反比例函数y=
 的图象中,y的值随x怎样变化?判断并说明理由.
的图象中,y的值随x怎样变化?判断并说明理由.
相关试题

