【题目】已知在△ABC中,AC=BC,AC⊥BC于点C,过点C作直线EF∥AB,点D在直线EF上,连接BD,过点D作GD⊥BD,交直线AC于点H,连接BG.
(1)如图1所示,当点D在射线CF上,点H在射线AC上时,连接BH,过点D作MD⊥CD,交CB的延长线于点M. 求证:∠GBH+∠G=∠M;
(2)如图2所示,当点D在射线CE上,点H在射线CA上时,试判断并证明DH与BD之间的数量关系.


图1 图2
参考答案:
【答案】(1)证明见解析; (2)DH=BD.
【解析】分析:(1)如图1中,作DN⊥EM于N,DP⊥AC于P.只要证明四边形PCND是矩形,△DPH≌△DNB,推出DH=BD,推出△BDH是等腰直角三角形,由此即可解决问题;(2)如图2中,作DN⊥BC于N,DP⊥AC于P.只要证明四边形PCND是矩形,△DPH≌△DNB即可;
本题解析:
(1)证明:如图1,作DN⊥EM于N,DP⊥AC于P.

∵CA=CB, ∠ACB=90°, ∴∠A=∠ABC=45°, ∵EF∥AB, ∴∠DCP=∠A=∠DCB=45°, ∵DN⊥EM于N,DP⊥AC于P, ∴DP=DN, ∵∠PCN=DNC=∠DPC=90°, ∴四边形PCND是矩形,∴∠PDN=BDH=90°, ∴PDH=BDN, ∴△DPH≌△DNB, ∴DH=BD, ∴△BDH是等腰直角三角形,∴∠BHD=45°, ∵∠BHD=∠GBH+∠G, ∴∠GBH+∠G=45°, ∵DM⊥DC, ∴∠M=∠DCM=45°, ∴∠GBH+∠G=∠M.
(2)如图2,作DN⊥BC于N,DP⊥AC于P,

∵CA=CB, ∠ACB=90°, ∴∠BCA=∠ABC=45°, ∵EF∥AB, ∴∠DCP=∠BAC=∠DCN=45°, ∵DN⊥EM于N,DP⊥AC于P, ∴DP=DN, ∵∠PCN=∠DNC=∠DPC=90°, ∴四边形PCND是矩形,∴∠PDN=∠BDH=90°, ∴∠PDH=∠BDN, ∴△DPH≌△DNB, ∴DH=BD.
点睛:本题考查了等腰直角三角形的性质.平行线的性质、全等三角形的判定与性质、矩形的判定与性质等知识点,能添加常用辅助线,构造全等三角形解决问题,是解本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2+bx与x轴交于O,A(4,0)两点,点B的坐标为(0,-3).
(1)求抛物线的对称轴;
(2)已知点P在抛物线的对称轴上,连接OP,BP. 若要使OP+BP的值最小,求出点P的坐标;
(3)将抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象. 当直线y=x+m(m≠0)与这个新图象有两个公共点时,在反比例函数y=
 的图象中,y的值随x怎样变化?判断并说明理由.
的图象中,y的值随x怎样变化?判断并说明理由.
-
科目: 来源: 题型:
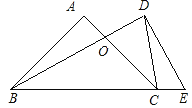
查看答案和解析>>【题目】将一副直角三角板如图摆放,等腰直角三角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同,且斜边BC与BE在同一直线上,AC与BD交于点O,连接CD.
求证:△CDO是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把代数式2x2﹣18分解因式,结果正确的是( )
A.2(x2﹣9)
B.2(x﹣3)2
C.2(x+3)(x﹣3)
D.2(x+9)(x﹣9) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标平面内,已知点A(8,0),点B(3,0),点C是点A关于直线m(直线m上各点的横坐标都为3)的对称点.
(1)在图中标出点A,B,C的位置并求出点C的坐标;
(2)如果点P在y轴上,过点P作直线l∥x轴,点A关于直线l的对称点是点D,那么当△BCD的面积等于10时,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学习小组13名学生的一次英语听力测试成绩分布如下表所示(满分20分):
成绩(分)
14
15
16
17
18
19
20
人数(人)
1
3
2
2
1
2
2
这13名学生听力测试成绩的中位数是( )
A.16分
B.17分
C.18分
D.19分 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件发生的可能性为0的是( )
A.掷两枚骰子,同时出现数字“6”朝上
B.小明从家里到学校用了10分钟,从学校回到家里却用了15分钟
C.今天是星期天,昨天必定是星期六
D.小明步行的速度是每小时50千米
相关试题

