【题目】如图:△ABC和△ADE是等边三角形,AD是BC边上的中线.求证:BE=BD.

参考答案:
【答案】证明见解析.
【解析】试题分析:根据等边三角形三线合一的性质可得AD为∠BAC的角平分线,根据等边三角形各内角为60°即可求得∠BAE=∠BAD=30°,进而证明△ABE≌△ABD,得BE=BD.
试题解析:(方法1)证明:∵△ABC和△ADE都是等边三角形
∴∠DAE=∠BAC=60°∴∠EAB=∠DAC
∵AE=AD,AB=AC
∴△ABE≌△ACD(SAS)
∴BE="CD"
∵AD是△ABC的中线
∴BD="CD"
∴BE=BD
(方法2)证明:∵△ABC是等边三角形,
∴∠BAC=60°
∵AD为BC边上的中线,
∴AD平分∠BAC.
即∠BAD=∠DAC=![]() ∠BAC=30°,
∠BAC=30°,
又∵△ADE为等边三角形,
∴AE=AD=ED,且∠EAD=60°,
而∠BAD=30°,
∴∠EAB=∠EAD﹣∠BAD=30°.
∴∠EAB=∠BAD.
∴AB垂直平分DE,
∴BE=BD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下列结论:①△ABD≌△EBC;②AC=2CD;③AD=AE=EC;④∠BCE+∠BCD=180°.其中正确的是
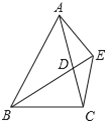
A. ①②③ B. ①②④ C. ①③④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程kx2+2x+1=0有实数根,则k的取值范围是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面给出的四个语句,其中正确的有( )
①等角的余角相等;
②一个角的补角一定大于这个角;
③有理数分为正数和负数;
④零是最小的正数;
⑤过直线外一点可以作一条以上的直线与已知直线平行.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一个外角等于130°,则这个等腰三角形的底角为( )
A. 65° B. 50° C. 65°或40° D. 50°或65°
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x的相反数是2,|y|=6,则x+y的值是( )
A. ﹣8 B. 4 C. ﹣8或4 D. 8或4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知动点P以每秒2cm的速度沿图甲的边框按BCDEFA的路径移动,相应的三角形ABP的面积S(cm2)与时间t(秒)之间的关系用图乙中的图象表示,若AB=6cm,试回答下列问题:
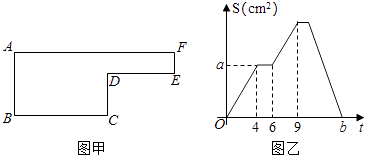
(1)图甲中的BC长是多少?
(2)图乙中的a是多少?
相关试题

