搜索
【题目】已知，如图点A（1，1），B（2，﹣3），点P为x轴上一点，当|PA﹣PB|最大时，点P的坐标为（ ）
A. （﹣1，0） B. （
，0） C. （
，0） D. （1，0）
参考答案：
【答案】B
【解析】
作A关于x轴对称点C，连接BC并延长，BC的延长线与x轴的交点即为所求的P点；首先利用待定系数法即可求得直线BC的解析式，继而求得点P的坐标．
作A关于x轴对称点C，连接BC并延长交x轴于点P，
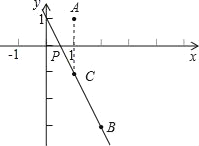
∵A（1，1），
∴C的坐标为（1，﹣1），
连接BC，
设直线BC的解析式为：y＝kx+b，
∴
，
解得：
，
∴直线BC的解析式为：y＝﹣2x+1，
当y＝0时，x＝
，
∴点P的坐标为：（，0），
∵当B，C，P不共线时，根据三角形三边的关系可得：|PA﹣PB|＝|PC﹣PB|＜BC，
∴此时|PA﹣PB|＝|PC﹣PB|＝BC取得最大值．
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，A（a，0），C（b，2），且满足（a+2）2+
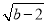＝0，过点C作CB⊥x轴于点B．（1）求A、C两点坐标；
（2）若过点B作BD∥AC交y轴于点D，且AE、DE分别平分∠CAB、∠ODB，如图2，求∠AED的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AC=BC，∠ACB=90°，点D在BC延长线上，连接AD，过B作BE⊥AD，垂足为E，交AC于点F，连接CE．
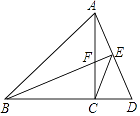
（1）求证：CF=CD；
（2）求证：DADE=DBDC；
（3）探究线段AE，BE，CE之间满足的等量关系，并说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】某地区经过一年的新农村建设，农村的经济收入增加了一倍，实现翻番，为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例，得到如下统计图：
建设前经济收入构成比例统计图 建设后经济收入构成比例统计图
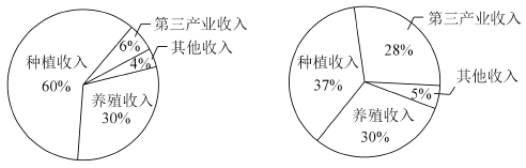
则下面结论中不正确的是( )
A. 新农村建设后，养殖收入增加了一倍
B. 新农村建设后，种植收入减少
C. 新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半
D. 新农村建设后，其他收入增加了一倍以上
-
科目： 来源： 题型：
查看答案和解析>>【题目】某学校在暑假期间开展“心怀感恩，孝敬父母”的实践活动，倡导学生在假期中帮助父母干家务，开学以后，校学生会随机抽取了部分学生，就暑假“平均每天帮助父母干家务所用时长”进行了调查，以下是根据相关数据绘制的统计图的部分：
根据上述信息，回答下列问题：
在本次随机抽取的样本中，调查的学生人数是 人；
，
；
补全频数分布直方图；
如果该校共有学生
人，请你估计“平均每天帮助父母干家务的时长不少于
分钟”的学生大约有多少人？ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：抛物线C1：y=x2﹣2a x+2a+2 顶点P在另一个函数图象C2上
（1）求证：抛物线C1必过定点A（1，3）；并用含的a式子表示顶点P的坐标；
（2）当抛物线C1的顶点P达到最高位置时，求抛物线C1解析式；并判断是否存在实数m、n，当m≤x≤n时恰有3m≤y≤3n，若存在，求出求m、n的值；若不存在，说明理由；
（3）抛物线C1和图象C2分别与y轴交于B、C点，当△ABC为等腰三角形，求a的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在等边三角形ABC中，AD＝BE＝CF，D、E、F不是各边的中点，AE、BF、CD分别交于P、M、H，如果把三个三角形全等叫做一组全等三角形，那么图中全等三角形有（ ）
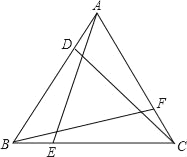
A. 6组 B. 5组 C. 4组 D. 3组
相关试题
