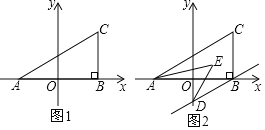
【题目】如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+![]() =0,过点C作CB⊥x轴于点B.
=0,过点C作CB⊥x轴于点B.
(1)求A、C两点坐标;
(2)若过点B作BD∥AC交y轴于点D,且AE、DE分别平分∠CAB、∠ODB,如图2,求∠AED的度数.
参考答案:
【答案】(1)A(﹣2,0),C(2,2);(2)∠AED的度数为45°.
【解析】
(1)根据偶次方和绝对值的非负性,可求得a、b的值,则A、C两点坐标可以求出;
(2)根据平行线的性质,得∠CAB+∠ODB=∠5+∠6=90°,再根据AE、DE分别平分∠CAB、∠ODB,得∠1=∠3=![]() ∠CAB,∠2=∠4=
∠CAB,∠2=∠4=![]() ∠ODB,最后根据∠AED=∠1+∠2可求得的度数.
∠ODB,最后根据∠AED=∠1+∠2可求得的度数.
(1)∵(a+2)2+![]() =0
=0
∴a+2=0,b﹣2=0,
∴a=﹣2,b=2,
∴A(﹣2,0),C(2,2);
(2)∵CB∥y轴,BD∥AC,
∴∠CAB=∠5,∠ODB=∠6,
∴∠CAB+∠ODB=∠5+∠6=90°,
过点E作EF∥AC,如图
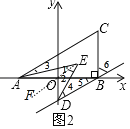
∵BD∥AC
∴BD∥EF∥AC,
∵AE、DE分别平分∠CAB、∠ODB,
∴∠1=∠3=![]() ∠CAB,∠2=∠4=
∠CAB,∠2=∠4=![]() ∠ODB,
∠ODB,
∴∠AED=∠1+∠2=![]() (∠CAB+∠ODB)=45°
(∠CAB+∠ODB)=45°
∴∠AED的度数为45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=
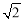 ,求AD的长.
,求AD的长.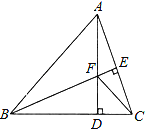
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为40和28,则△EDF的面积为( )
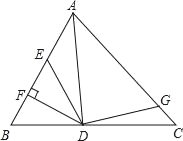
A. 12 B. 6 C. 7 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB和直线CD相交于O点,OE⊥OD,OF平分∠AOE,∠BOD=26°
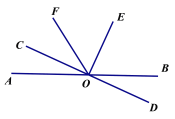
(1)写出∠COB的邻补角。
(2)求∠COF的度数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.
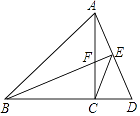
(1)求证:CF=CD;
(2)求证:DADE=DBDC;
(3)探究线段AE,BE,CE之间满足的等量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下统计图:
建设前经济收入构成比例统计图 建设后经济收入构成比例统计图
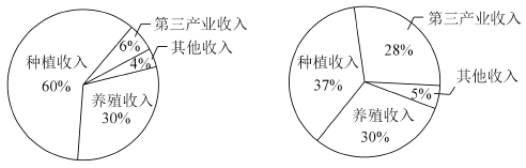
则下面结论中不正确的是( )
A. 新农村建设后,养殖收入增加了一倍
B. 新农村建设后,种植收入减少
C. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
D. 新农村建设后,其他收入增加了一倍以上
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图点A(1,1),B(2,﹣3),点P为x轴上一点,当|PA﹣PB|最大时,点P的坐标为( )

A. (﹣1,0) B. (
 ,0) C. (
,0) C. ( ,0) D. (1,0)
,0) D. (1,0)
相关试题

