【题目】探究题：已知：如图,,.求证：.

老师要求学生在完成这道教材上的题目证明后，尝试对图形进行变形，继续做拓展探究，看看有什么新发现？

（1）小颖首先完成了对这道题的证明，在证明过程中她用到了平行线的一条性质，小颖用到的平行线性质可能是 .

（2）接下来，小颖用《几何画板》对图形进行了变式，她先画了两条平行线，然后在平行线间画了一点，连接后，用鼠标拖动点，分别得到了图，小颖发现图正是上面题目的原型，于是她由上题的结论猜想到图和图中的与之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能，找到了这三个角之间的数量关系.

请你在小颖操作探究的基础上，继续完成下面的问题：

（ⅰ）猜想图中与之间的数量关系并加以证明；

（ⅱ）补全图，直接写出与之间的数量关系： .

参考答案：

【答案】（1）两直线平行同旁内角互补；（2）（ⅰ），见解析；（ⅱ）见解析，.

【解析】

（1）根据两直线平行同旁内角互补即可解决问题；
（2）（ⅰ）猜想∠BDF=∠B+∠F．过点D作CD∥AB．利用平行线的性质即可解决问题；
（ⅱ）∠BDF与∠F之间的数量关系是∠F=∠B+∠BDF．利用平行线的性质已经三角形的外角的性质即可解决问题；

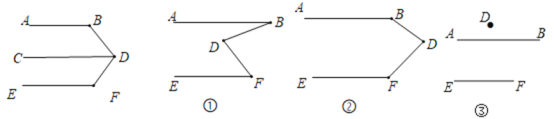
解：（1）∵AB//CD，

∴∠B+∠BDC=180°(两直线平行，同旁内角互补)，

∵CD//EF(已知)，
∴∠CDF+∠DFE=180°(两直线平行，同旁内角互补)，
∴∠B+∠BDF+∠F=∠B+∠BDC+∠CDF+∠DFE=360°．

故答案为:两直线平行同旁内角互补．

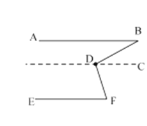
(2)（ⅰ）猜想

证明：过点作，

,

（ⅱ）补全图形如图所示：∠B、∠BDF与∠F之间的数量关系是∠F=∠B+∠BDF．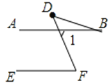

理由：∵AB∥EF，
∴∠1=∠F，
∵∠1=∠B+∠D，
∴∠F=∠B+∠BDF．
故答案为∠F=∠B+∠BDF．

关闭