【题目】如图,一副三角板![]() 和
和![]() 拼合在一起,边
拼合在一起,边![]() 与
与![]() 重合,
重合,![]() ,
,![]() ,
,![]() ,
,![]() .当点
.当点![]() 从点
从点![]() 出发沿
出发沿![]() 向下滑动时,点
向下滑动时,点![]() 同时从点
同时从点![]() 出发沿射线
出发沿射线![]() 向右滑动.当点
向右滑动.当点![]() 从点
从点![]() 滑动到点
滑动到点![]() 时,连接
时,连接![]() ,则
,则![]() 的面积最大值为_______
的面积最大值为_______![]() .
.

参考答案:
【答案】![]()
【解析】
根据勾股定理分别求出BC和FD的长度,再根据题意得出点D到BC的最大距离为DF,计算即可得出答案.
在Rt△ABC中,∠BAC=30°,∠ACB=90°,AC=6cm
可设CB=xcm,AB=2xcm
根据勾股定理可得![]()
∴BC=2![]() cm
cm
在Rt△EDF中,∠EDF=90°,∠DEF=45°,EF=AC=6cm
可设ED=FD=ycm
可得![]()
∴DF=ED=3![]() cm
cm
在点F从点C出发沿射线BC向右滑动的过程中,当DF⊥BC时,点D到BC的距离最大最大值为DF,
此时![]() ,
,
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,延长
中,延长 至
至 使
使 ,以
,以 为边作正方形
为边作正方形 ,延长
,延长 交
交 于
于 ,连接
,连接 ,
, ,
, 为
为 的中点,连接
的中点,连接 分别与
分别与 ,
, 交于点
交于点 .则下列说法:①
.则下列说法:① ;②
;② ;③
;③ ;④
;④ .其中正确的有( )
.其中正确的有( )
A.4个B.3个C.2个D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究题:已知:如图,
 ,
,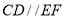 .求证:
.求证: .
.
老师要求学生在完成这道教材上的题目证明后,尝试对图形进行变形,继续做拓展探究,看看有什么新发现?
(1)小颖首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小颖用到的平行线性质可能是 .
(2)接下来,小颖用《几何画板》对图形进行了变式,她先画了两条平行线
 ,然后在平行线间画了一点
,然后在平行线间画了一点 ,连接
,连接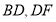 后,用鼠标拖动点
后,用鼠标拖动点 ,分别得到了图
,分别得到了图
 ,小颖发现图
,小颖发现图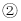 正是上面题目的原型,于是她由上题的结论猜想到图
正是上面题目的原型,于是她由上题的结论猜想到图 和
和 图中的与
图中的与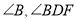 之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.请你在小颖操作探究的基础上,继续完成下面的问题:
(ⅰ)猜想图
 中
中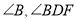 与
与 之间的数量关系并加以证明;
之间的数量关系并加以证明;(ⅱ)补全图
 ,直接写出
,直接写出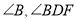 与
与 之间的数量关系: .
之间的数量关系: . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,以
 的斜边
的斜边 为边,在
为边,在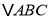 的同侧作正方形
的同侧作正方形 ,
, ,
, 交于点
交于点 ,连接
,连接 .若
.若 ,
, ,则
,则 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
 中,
中, ,
, ,点
,点 是
是 边的中点,点
边的中点,点 是
是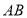 边上一动点(不与点
边上一动点(不与点 重合),延长
重合),延长 交射线
交射线 于点
于点 ,连接
,连接 ,
, .
.
(1)求证:四边形
 是平行四边形;
是平行四边形;(2)填空:
①当
 的值为_______时,四边形
的值为_______时,四边形 是矩形;
是矩形;②当
 的值为______时,四边形
的值为______时,四边形 是菱形.
是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一个单位面积为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,……是斜边在x轴上,且斜边长分别为2,4,6,……的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,点A2019的横坐标为( )
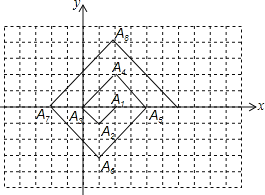
A. 1010B.
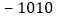 C. 1008D.
C. 1008D. 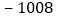
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:(1)
 (用代入消元法);(2)
(用代入消元法);(2)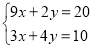 (用加减消元法)
(用加减消元法)
相关试题

