【题目】某学校为美化校园,准备在长35米,宽20米的长方形场地上,修建若干条宽度相同的道路,余下部分作草坪,并请全校学生参与方案设计,现有3位同学各设计了一种方案,图纸分别如图l、图2和图3所示(阴影部分为草坪).

请你根据这一问题,在每种方案中都只列出方程不解.
①甲方案设计图纸为图l,设计草坪的总面积为600平方米.
②乙方案设计图纸为图2,设计草坪的总面积为600平方米.
③丙方案设计图纸为图3,设计草坪的总面积为540平方米.
参考答案:
【答案】见解析.
【解析】试题分析:①设道路的宽为x米.长应该为35﹣2x,宽应该为20﹣2x;那么根据草坪的面积为600m2 ,即可得出方程;
②如果设路宽为xm,草坪的长应该为35﹣x,宽应该为20﹣x;那么根据草坪的面积为600m2,即可得出方程;
③如果设路宽为xm,草坪的长应该为35﹣2x,宽应该为20﹣x;那么根据草坪的面积为540m2 , 即可得出方程.
试题解析:①设道路的宽为x米.依题意得:(35﹣2x)(20﹣2x)=600;
②设道路的宽为x米.依题意得:(35﹣x)(20﹣x)=600;
③设道路的宽为x米.依题意得:(35﹣2x)(20﹣x)=540.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据不等式的性质,可以得到:若a-b>0,则a>b;若a-b=0,则a=b;若a-b<0,则a<b.这是利用“作差法”比较两个数或两个代数式值的大小.已知A=5m2-4(
 m-
m-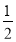 ),B=7(m2-m)+3,请你运用前面介绍的方法比较代数式A与B的大小.
),B=7(m2-m)+3,请你运用前面介绍的方法比较代数式A与B的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图四边形ABCD是一块草坪,量得四边长AB=3m,BC=4m,DC=12m,AD=13m,∠B=90°,求这块草坪的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】统计七年级部分同学的跳高测试成绩,得到如下频率直方图(每组含前一个边界值,不含后一个边界值).

(1)参加测试的总人数是多少人?
(2)组距为多少?
(3)跳高成绩在
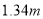 (含
(含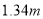 )以上的有多少人?占总人数的百分之几?
)以上的有多少人?占总人数的百分之几? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD是平行四边形,延长BA至点E,使AE=AB,连接CE、DE、AC,CE与AD交于点F.

(1)求证:四边形ACDE是平行四边形;
(2)若∠AFC=2∠B.求证:四边形ACDE是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,延长
中,延长 至
至 使
使 ,以
,以 为边作正方形
为边作正方形 ,延长
,延长 交
交 于
于 ,连接
,连接 ,
, ,
, 为
为 的中点,连接
的中点,连接 分别与
分别与 ,
, 交于点
交于点 .则下列说法:①
.则下列说法:① ;②
;② ;③
;③ ;④
;④ .其中正确的有( )
.其中正确的有( )
A.4个B.3个C.2个D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究题:已知:如图,
 ,
,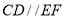 .求证:
.求证: .
.
老师要求学生在完成这道教材上的题目证明后,尝试对图形进行变形,继续做拓展探究,看看有什么新发现?
(1)小颖首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小颖用到的平行线性质可能是 .
(2)接下来,小颖用《几何画板》对图形进行了变式,她先画了两条平行线
 ,然后在平行线间画了一点
,然后在平行线间画了一点 ,连接
,连接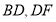 后,用鼠标拖动点
后,用鼠标拖动点 ,分别得到了图
,分别得到了图
 ,小颖发现图
,小颖发现图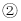 正是上面题目的原型,于是她由上题的结论猜想到图
正是上面题目的原型,于是她由上题的结论猜想到图 和
和 图中的与
图中的与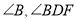 之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.请你在小颖操作探究的基础上,继续完成下面的问题:
(ⅰ)猜想图
 中
中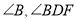 与
与 之间的数量关系并加以证明;
之间的数量关系并加以证明;(ⅱ)补全图
 ,直接写出
,直接写出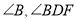 与
与 之间的数量关系: .
之间的数量关系: .
相关试题

