【题目】如图,已知一次函数![]() 的图象与坐标轴分别交于A、B点,AE平分
的图象与坐标轴分别交于A、B点,AE平分![]() ,交
,交![]() 轴于点E.
轴于点E.

(1)直接写出点A和点B的坐标.
(2)求直线AE的表达式.
(3)过点B作BF![]() AE于点F,过点F分别作FD//OA交AB于点D,FC//AB交
AE于点F,过点F分别作FD//OA交AB于点D,FC//AB交![]() 轴于点C,判断四边形ACFD的形状并说明理由,求四边形ACFD的面积.
轴于点C,判断四边形ACFD的形状并说明理由,求四边形ACFD的面积.
参考答案:
【答案】(1)A(0,6),B(8,0);(2)y=2x+6;(3)四边形ACFD是菱形,证明见解析;S四边形ACFD=20
【解析】
(1)一次函数![]() ,令x=0求出y值,可得A点坐标,令y=0,求出x值,可得B点坐标,此题得解;
,令x=0求出y值,可得A点坐标,令y=0,求出x值,可得B点坐标,此题得解;
(2)已知A,B点坐标,结合勾股定理可求出AB的长度,再利用角平分线的性质即可求出点E的坐标,根据点A、E的坐标利用待定系数法即可求出直线AE的表达式;
(3)过点B作BF![]() AE于点F,过点F分别作FD//OA交AB于点D,FC//AB交
AE于点F,过点F分别作FD//OA交AB于点D,FC//AB交![]() 轴于点C,连接CD交AF于点G,可得四边形ACFD是平行四边形,证明AD=DF,即可得到四边形ACFD是菱形,证明△AOE∽△BFE,即可得到
轴于点C,连接CD交AF于点G,可得四边形ACFD是平行四边形,证明AD=DF,即可得到四边形ACFD是菱形,证明△AOE∽△BFE,即可得到![]() ,
,![]() ,求得BF和EF,进而求得四边形ACFD的面积.
,求得BF和EF,进而求得四边形ACFD的面积.
(1)∵![]()
当x=0时,y=6
∴A(0,6)
当y=0时,![]()
解得x=8
∴B(8,0)
∴A(0,6),B(8,0)
(2)过点E作EM⊥AB于D
∴OA=6,OB=8,
∴AB=![]()
∵AE平分∠BAO,交x轴于点E
∴OE=ME
∴![]()
∴![]()
∴OE=![]() BE
BE
∵OE+BE=OB=8
∴OE=3,BE=5
∴点E的坐标为(3,0)
设直线AE的表达式为y=kx+b
将A(0,6)、E(3,0)代入y=kx+b
![]()
解得:![]()
∴直线AE的表达式为y=2x+6

(3)过点B作BF![]() AE于点F,过点F分别作FD//OA交AB于点D,FC//AB交
AE于点F,过点F分别作FD//OA交AB于点D,FC//AB交![]() 轴于点C,连接CD交AF于点G
轴于点C,连接CD交AF于点G
∵FD//OA,FC//AB
∴四边形ACFD是平行四边
∴∠CAF=∠AFD
∵∠CAF=∠FAD
∴∠AFD=∠FAD
∴AD=DF
∴四边形ACFD是菱形
∵∠AOE=∠BFE=90°,∠AEO=∠BEF
∴△AOE∽△BFE
∴![]()
∵OE=3,OA=6
∴AE=![]()
∴![]()
∴BF=![]()
∵四边形ACFD是菱形
∴DG⊥AF,AG=GF
∴DG=![]() BF=
BF=![]()
∵![]()
∴![]()
∴EF=![]()
∴AF=AE+EF=![]()
S四边形ACFD=AF×DG=![]()
故答案为:四边形ACFD是菱形,证明见解析;S四边形ACFD=20

-
科目: 来源: 题型:
查看答案和解析>>【题目】为调查某校初二学生一天零花钱的情况,随机调查了初二级部分学生的零钱金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列问题:

(1)本次接受随机抽样调查的学生人数为_____,图①中
 的值是_____;
的值是_____;(2)求本次调查获取的样本数据的平均数;
(3)根据样本数据,估计该年级300名学生每天零花钱不多于10元的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
 的图象过点A(0,3)和点B(3,0),且与正比例函数
的图象过点A(0,3)和点B(3,0),且与正比例函数 的图象交于点P.
的图象交于点P.
(1)求函数
 的解析式和点P的坐标.
的解析式和点P的坐标.(2)画出两个函数 的图象,并直接写出当
 时
时 的取值范围.
的取值范围.(3)若点Q是
 轴上一点,且△PQB的面积为8,求点Q的坐标.
轴上一点,且△PQB的面积为8,求点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,已知AB=AC,D是AC上的一点,CD=9,BC=15,BD=12.

(1)判断△BCD的形状并证明你的结论.
(2)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在这段时间内,线段PQ平行于AB的次数是( )

A.2B.3C.4D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列单项式:
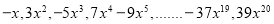 ,回答下列问题:
,回答下列问题:(1)这组单项式的系数符号的规律是 。
(2)这组单项式系数绝对值的规律是 。
(3)这组单项式的次数规律是 。
(4)写出第2017,2018个单项式 , 。
(5)写出第n个单项式 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1) 2(2a 2 9b) 3(3a 2 4b)
(2)(
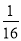 a 2 b2)(
a 2 b2)(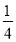 a b)(
a b)( 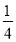 a b)
a b)(3) (
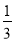 x 2y 3 )2 (3xy)3 (
x 2y 3 )2 (3xy)3 (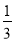 x 2 y 3)2 ( x)3 2 y 3
x 2 y 3)2 ( x)3 2 y 3(4)用简便方法计算:9982 9980 16
相关试题

