搜索
【题目】如图，△ABC中，已知AB=AC，D是AC上的一点，CD=9，BC=15，BD=12．
（1）判断△BCD的形状并证明你的结论．
（2）求△ABC的面积．
参考答案：
【答案】（1）见解析；（2）75
【解析】
（1）利用勾股定理的逆定理即可直接证明△BCD是直角三角形；
（2）设AD=x，则AC=x+9，在直角△ABD中，利用勾股定理即可列出方程，解方程，即可求解．
（1）∵CD=9，BD=12
∴CD2+BD2=81+144=225
∵BC=15
∴BC2=225
∴CD2+BD2=BC2
∴△BCD是直角三角形
（2）设AD=x，则AC=x+9
∵AB=AC
∴AB=x+9
∵∠BDC=90°
∴∠ADB=90°
∴AB2=AD2+BD2
即(x+9)2=x2+122
解得：x=
∴AC=+9=
∴S△ABC=
ACBD=
=75
故答案为：75
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算
(1)6－（＋3）－（－7）＋（－2）;
(2)(－
－
＋
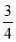)×(－36)(3) (﹣2)2+3×（﹣1）2016﹣（﹣4）×2 .
(4)6x2y－(－2x2y)
(5)(3a－2) －2(a－1)
-
科目： 来源： 题型：
查看答案和解析>>【题目】为调查某校初二学生一天零花钱的情况，随机调查了初二级部分学生的零钱金额，并用得到的数据绘制了如下统计图①和图②，请根据相关信息，解答下列问题：
（1）本次接受随机抽样调查的学生人数为_____,图①中
的值是_____；（2）求本次调查获取的样本数据的平均数；
（3）根据样本数据，估计该年级300名学生每天零花钱不多于10元的学生人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一次函数
的图象过点A（0，3）和点B（3，0），且与正比例函数
的图象交于点P．
（1）求函数
的解析式和点P的坐标．（2）画出两个函数 的图象，并直接写出当
时
的取值范围．（3）若点Q是
轴上一点，且△PQB的面积为8，求点Q的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知一次函数
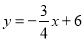的图象与坐标轴分别交于A、B点，AE平分
，交
轴于点E．
（1）直接写出点A和点B的坐标．
（2）求直线AE的表达式．
（3）过点B作BF
AE于点F，过点F分别作FD//OA交AB于点D，FC//AB交
轴于点C，判断四边形ACFD的形状并说明理由，求四边形ACFD的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，AB＝4cm，AD＝12cm，点P在AD边上以每秒1cm的速度从点A向点D运动，点Q在BC边上，以每秒4cm的速度从点C出发，在CB间往返运动，两个点同时出发，当点P到达点D时停止（同时点Q也停止），在这段时间内，线段PQ平行于AB的次数是（ ）
A.2B.3C.4D.5
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察下列单项式：
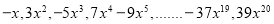，回答下列问题：（1）这组单项式的系数符号的规律是 。
（2）这组单项式系数绝对值的规律是 。
（3）这组单项式的次数规律是 。
（4）写出第2017，2018个单项式 ， 。
（5）写出第n个单项式 。
相关试题
