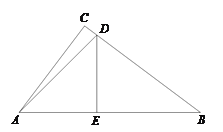
【题目】如图,在Rt△ABC中,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ⊥
⊥![]() ,点
,点![]() 为垂足,
为垂足,![]() ,∠DAB=450,tanB=
,∠DAB=450,tanB=![]() .
.
(1)求![]() 的长;
的长;
(2)求![]() 的余弦值.
的余弦值.
参考答案:
【答案】(1)3;(2)![]()
【解析】分析:(1)由题意得到三角形ADE为等腰直角三角形,在直角三角形DEB中,利用锐角三角函数定义求出DE与BE之比,设出DE与BE,由AB=7求出各自的值,确定出DE即可;
(2)在直角三角形中,利用勾股定理求出AD与BD的长,根据tanB的值求出cosB的值,确定出BC的长,由BC﹣BD求出CD的长,利用锐角三角函数定义求出所求即可.
详解:(1)∵DE⊥AB,∴∠DEA=90°.又∵∠DAB=45°,∴DE=AE.在Rt△DEB中,∠DEB=90°,tanB=![]() =
=![]() ,设DE=3x,那么AE=3x,BE=4x.∵AB=7,∴3x+4x=7,解得:x=1,∴DE=3;
,设DE=3x,那么AE=3x,BE=4x.∵AB=7,∴3x+4x=7,解得:x=1,∴DE=3;
(2)在Rt△ADE中,由勾股定理,得:AD=3![]() ,同理得:BD=5.在Rt△ABC中,由tanB=
,同理得:BD=5.在Rt△ABC中,由tanB=![]() ,可得:cosB=
,可得:cosB=![]() ,∴BC=
,∴BC=![]() ,∴CD=
,∴CD=![]() ,∴cos∠CDA=
,∴cos∠CDA=![]() =
=![]() ,即∠CDA的余弦值为
,即∠CDA的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】记Sn=a1+a2+…+an,令Tn=
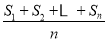 ,称Tn为a1,a2,…,an这列数的“神秘数”.已知a1,a2,…,a500的“神秘数”为1503,那么6,a1,a2,…,a500的“神秘数”为( )
,称Tn为a1,a2,…,an这列数的“神秘数”.已知a1,a2,…,a500的“神秘数”为1503,那么6,a1,a2,…,a500的“神秘数”为( )A.1504B.1506C.1508D.1510
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有20箱苹果,以每箱25千克为标准,超过的千克数用正数表示,不足的千克数用负数表示,结果记录如表:
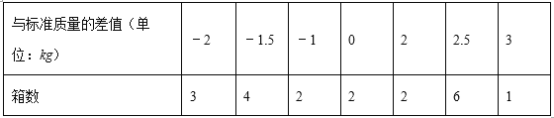
(1)20箱苹果中,最重的一箱比最轻的一箱重 kg;
(2)与标准质量相比,20箱苹果总计超过或不足多少千克?
(3)若苹果每千克售价12元,则售出这20箱苹果可获得多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】1952个正整数1,2,3,4,…,1952按如图方式排列成一个表:
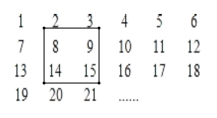
(1)如图,用一正方形方框任意框住4个数,记左上角的一个数为x,当被框住的4个数之和等于358时,x的值为多少?
(2)如(1)中方式,能否框住这样的4个数,它们的和等于2438?若能,则求出x的值;若不能,则说明理由.
(3)从左到右,第1到第6列各列数之和分别记为a1,a2,a3,a4,a5,a6,则这6个数中,最大数与最小数之差等于 .(直接填出结果,不写计算过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
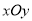 中,一次函数
中,一次函数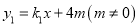 的图象
的图象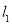 经过点
经过点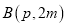 .
.(1)当
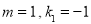 时,且正比例函数
时,且正比例函数 的图象
的图象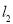 经过点
经过点 .
.①若
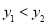 ,求
,求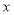 的取值范围;
的取值范围;②若一次函数
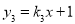 的图象为
的图象为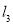 ,且
,且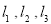 不能围成三角形,求
不能围成三角形,求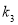 的值;
的值;(2)若直线
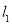 与
与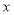 轴交于点
轴交于点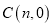 ,且
,且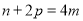 ,求
,求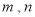 的数量关系.
的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程|x2﹣x|﹣a=0,给出下列四个结论:①存在实数a,使得方程恰有2个不同的实根; ②存在实数a,使得方程恰有3个不同的实根;③存在实数a,使得方程恰有4个不同的实根;④存在实数a,使得方程恰有6个不同的实根;其中正确的结论个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
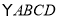 中,点
中,点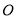 是对角线
是对角线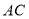 的中点,点
的中点,点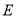 在
在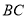 上,且
上,且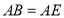 ,连接
,连接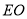 并延长交
并延长交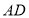 于点F.过点
于点F.过点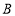 作
作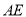 的垂线,垂足为
的垂线,垂足为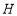 ,交
,交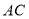 于点
于点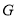 .
.(1)求证:
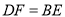 ;
;(2)若
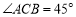 .
.①求证:
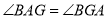 ;
;②探索
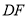 与
与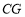 的数量关系,并说明理由.
的数量关系,并说明理由.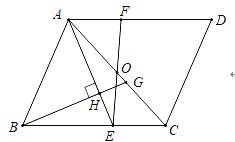
相关试题

