【题目】如图,在![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点F.过点
于点F.过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() .
.
①求证:![]() ;
;
②探索![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
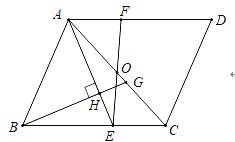
参考答案:
【答案】(1)见解析;(2)①见解析,②![]() ,理由见解析.
,理由见解析.
【解析】
(1)根据平行四边形的性质得到∠OAF=∠OCE,证明△OAF≌△OCE,根据全等三角形的对应边相等证明结论;
(2)①过A作AM⊥BC于M,交BG于K,过G作GN⊥BC于N,根据三角形的外角性质得到∠BAG=∠BGA;
②证明△AME≌△BNG,根据全等三角形的性质得到ME=NG,根据等腰直角三角形的性质得到BE=![]() GC,根据(1)中结论证明即可.
GC,根据(1)中结论证明即可.
(1)证明:∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
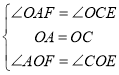 ,
,
∴![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
(2)①过![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
则![]() ,
,
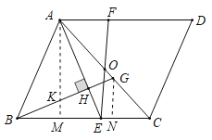
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,
,
设![]() ,
,
则![]() ,
,![]() ,
,
∴![]() ;
;
②![]() ,
,
理由如下:∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
在等腰![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,
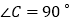 ,点
,点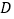 在边
在边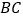 上,
上,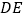 ⊥
⊥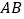 ,点
,点 为垂足,
为垂足,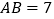 ,∠DAB=450,tanB=
,∠DAB=450,tanB=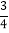 .
.(1)求
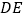 的长;
的长;(2)求
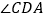 的余弦值.
的余弦值.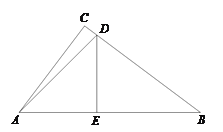
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
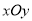 中,一次函数
中,一次函数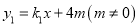 的图象
的图象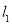 经过点
经过点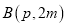 .
.(1)当
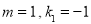 时,且正比例函数
时,且正比例函数 的图象
的图象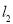 经过点
经过点 .
.①若
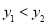 ,求
,求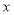 的取值范围;
的取值范围;②若一次函数
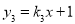 的图象为
的图象为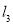 ,且
,且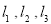 不能围成三角形,求
不能围成三角形,求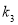 的值;
的值;(2)若直线
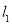 与
与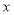 轴交于点
轴交于点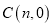 ,且
,且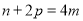 ,求
,求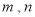 的数量关系.
的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程|x2﹣x|﹣a=0,给出下列四个结论:①存在实数a,使得方程恰有2个不同的实根; ②存在实数a,使得方程恰有3个不同的实根;③存在实数a,使得方程恰有4个不同的实根;④存在实数a,使得方程恰有6个不同的实根;其中正确的结论个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )
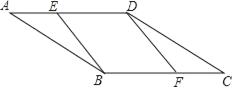
A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )

A.
 B. 1 C.
B. 1 C.  D. 2
D. 2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点A表示数a,点C表示数c,且|a+10|+(c﹣20)2=0.我们把数轴上两点之间的距离用表示两点的大写字母一起标记,比如,点A与点B之间的距离记作AB.

(1)求a、c的值;
(2)已知点D为数轴上一动点,且满足CD+AD=32,直接写出点D表示的数;
(3)动点B从数1对应的点开始向右运动,速度为每秒1个单位长度.同时点A、C在数轴上运动,点A、C的速度分别为每秒3个单位长度、每秒4个单位长度,运动时间为t秒:
①若点A向右运动,点C向左运动,AB=BC,求t的值;
②若点A向左运动,点C向右运动,2AB﹣m×BC的值不随时间t的变化而改变,请求出m的值.
相关试题

