【题目】在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象
的图象![]() 经过点
经过点![]() .
.
(1)当![]() 时,且正比例函数
时,且正比例函数![]() 的图象
的图象![]() 经过点
经过点![]() .
.
①若![]() ,求
,求![]() 的取值范围;
的取值范围;
②若一次函数![]() 的图象为
的图象为![]() ,且
,且![]() 不能围成三角形,求
不能围成三角形,求![]() 的值;
的值;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,求
,求![]() 的数量关系.
的数量关系.
参考答案:
【答案】(1)①![]() ;②
;②![]() 的值为
的值为![]() 或1或
或1或![]() ;(2)
;(2)![]() .
.
【解析】
(1)用待定系数法求出B点坐标,再求得正比例函数解析式,①由函数值的大小关系列出x的不等式,便可求得x的取值范围;②当l3过l1与l2的交点和l3与l1或l2平行时,l1,l2,l3不能围成三角形,由此求出k3;
(2)根据题意求得k1=-2,则y1=-2x+4m,代入(n,0),即可得到m,n的数量关系.
解:(1)依题意,得:![]() ,
,
图象![]() 经过点
经过点![]() ,
,
所以,![]() ,
,
解得:![]()
所以,![]() ,
,
正比例函数![]() 的图象
的图象![]() 经过点
经过点![]() ,
,
所以,![]() ,解得:
,解得:![]() ,
,
所以,![]() ,
,![]() 。
。
①若![]() ,则
,则![]() ,
,
解得,![]() ;
;
②若![]() ,
,![]() ,
,![]() 不能围成三角形,则
不能围成三角形,则![]() 或
或![]() ,或经过
,或经过![]() 与
与![]() 的交点,
的交点,
∵![]() 为:
为:![]() ,
,![]() 为
为![]() ,
,
解![]() ,解得
,解得![]() ,
,
∴交点![]() ,
,
代入![]() 得,
得,![]() ,
,
解得![]() ,
,
∴![]() 的值为
的值为![]() 或1或
或1或![]() ;
;
(2)∵一次函数![]() 的图象
的图象![]() 经过点
经过点![]() ,
,
∴![]() ①
①
直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
∴![]() ②
②
∴①×2+②得,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴一次函数为![]() ,
,
∵经过![]()
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有20箱苹果,以每箱25千克为标准,超过的千克数用正数表示,不足的千克数用负数表示,结果记录如表:
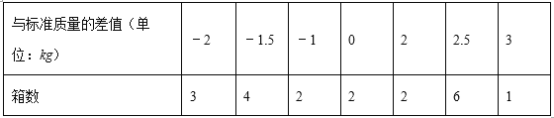
(1)20箱苹果中,最重的一箱比最轻的一箱重 kg;
(2)与标准质量相比,20箱苹果总计超过或不足多少千克?
(3)若苹果每千克售价12元,则售出这20箱苹果可获得多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】1952个正整数1,2,3,4,…,1952按如图方式排列成一个表:
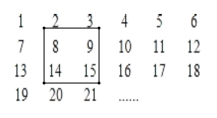
(1)如图,用一正方形方框任意框住4个数,记左上角的一个数为x,当被框住的4个数之和等于358时,x的值为多少?
(2)如(1)中方式,能否框住这样的4个数,它们的和等于2438?若能,则求出x的值;若不能,则说明理由.
(3)从左到右,第1到第6列各列数之和分别记为a1,a2,a3,a4,a5,a6,则这6个数中,最大数与最小数之差等于 .(直接填出结果,不写计算过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,
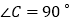 ,点
,点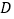 在边
在边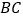 上,
上,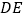 ⊥
⊥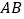 ,点
,点 为垂足,
为垂足,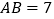 ,∠DAB=450,tanB=
,∠DAB=450,tanB=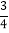 .
.(1)求
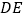 的长;
的长;(2)求
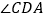 的余弦值.
的余弦值.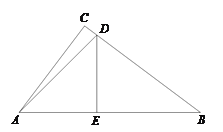
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程|x2﹣x|﹣a=0,给出下列四个结论:①存在实数a,使得方程恰有2个不同的实根; ②存在实数a,使得方程恰有3个不同的实根;③存在实数a,使得方程恰有4个不同的实根;④存在实数a,使得方程恰有6个不同的实根;其中正确的结论个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
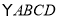 中,点
中,点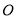 是对角线
是对角线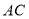 的中点,点
的中点,点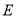 在
在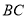 上,且
上,且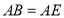 ,连接
,连接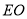 并延长交
并延长交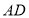 于点F.过点
于点F.过点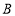 作
作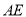 的垂线,垂足为
的垂线,垂足为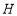 ,交
,交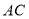 于点
于点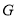 .
.(1)求证:
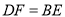 ;
;(2)若
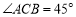 .
.①求证:
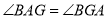 ;
;②探索
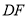 与
与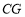 的数量关系,并说明理由.
的数量关系,并说明理由.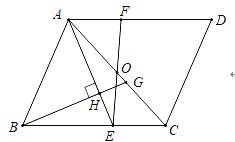
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )
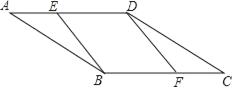
A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
相关试题

