搜索
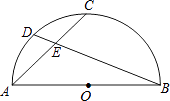
【题目】如图，AB是半圆O的直径，点C是 
的中点，点D是 
的中点，连接AC，BD交于点E，则 
=（ ）
A.
B.
C.1﹣ 
D.
参考答案：
【答案】D
【解析】连接AD、CD，作AF∥CD，交BE于F，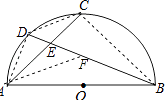
∵点D是弧AC的中点，
∴可设AD=CD=1，
根据平行线的性质得∠AFD=∠CDF=45°．
∴△ADF是等腰直角三角形，
则AF= 
，BF=AF= ．
∴BD= +1．
∵∠DAC=∠ABD，∠ADB=∠ADB，
∴△ADE∽△BDA，
∴DE= 
= ﹣1，BE=2．
∴ 
= 
．
所以答案是：D.
【考点精析】根据题目的已知条件，利用圆心角、弧、弦的关系和圆周角定理的相关知识可以得到问题的答案，需要掌握在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等；在同圆或等圆中，同弧等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半；顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB=
BC，连接OE．下列结论：①∠CAD=30°；②SABCD=ABAC；③OB=AB；④OE= 
BC，成立的个数有（ ）
A.1个
B.2个
C.3个
D.4个 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中有一个△ABC，顶点A（﹣1，3），B（2，0），C（﹣3，﹣1）．
（1）画出△ABC关于y轴的对称图形△A1B1C1（不写画法）；
点A关于x轴对称的点坐标为
点B关于y轴对称的点坐标为
点C关于原点对称的点坐标为
（2）若网格上的每个小正方形的边长为1，则△ABC的面积是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】看图填空：已知如图，AD⊥BC于D，EG⊥BC于G，∠E=∠3， 求证：AD平分∠BAC．
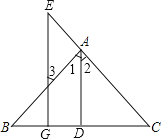
证明：∵AD⊥BC于D，EG⊥BC于G（ 已知 ）
∴∠ADC=90°，∠EGC=90°（ ）
∴∠ADC=∠EGC（等量代换）
∴AD∥EG（ ）
∴∠1=∠3（ ）
∠2=∠E（ ）
又∵∠E=∠3（ 已知） ∴∠1=∠2（ ）
∴AD平分∠BAC（ ）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，CD是AB边上的高，AC=4，BC=3，DB=
求：（1）求AD的长；
（2）△ABC是直角三角形吗？为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两名工人同时加工同一种零件，现根据两人7天产品中每天出现的次品数情况绘制成如下不完整的统计图和表，依据图、表信息，解答下列问题：
相关统计量表：
量数
人
众数
中位数
平均数
方差
甲
2
乙
1
1
1
次品数量统计表：
天数
人
1
2
3
4
5
6
7
甲
2
2
0
3
1
2
4
乙
1
0
2
1
1
0
（1）补全图、表．
（2）判断谁出现次品的波动小．
（3）估计乙加工该种零件30天出现次品多少件？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2），动点M沿路线O→A→C运动．
（1）求直线AB的解析式．
（2）求△OAC的面积．
（3）当△OMC的面积是△OAC的面积的
时，求出这时点M的坐标．
相关试题
