【题目】已知Rt△ABC≌Rt△DBE,∠ACB=∠DEB=90°,∠A=∠D.
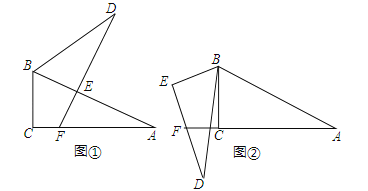
(1)将两三角形按图①方式摆放,其中点E落在AB上,DE所在直线交边AC于点F.求证:AF+EF=DE;
(2)若将两三角形按照图②方式摆放,边AC的延长线与DE相交于点F.你认为(1)中的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.
参考答案:
【答案】(1)证明见试题解析;(2)不成立.此时AF、EF与DE的关系为AF=EF+DE.
【解析】
试题分析:(1)由Rt△ABC≌Rt△DBE推出BC=BE,连接BF,由HL证Rt△BCF≌Rt△BEF,推出CF=EF即可;
(2)猜想(1)结论不成立,关系式是AF=EF+DE,连接BF,由HL证Rt△BEF≌Rt△BCF,推出EF=FC,由AF=AC+FC可推出AF=DE+EF.
试题解析:(1)证明:连接BF.由Rt△ABC≌Rt△DBE知:BC=BE.在Rt△BCF和Rt△BEF中,∵BC=BE,BF=BF,∴Rt△BCF≌Rt△BEF(HL),∴CF=EF,∵AC=DE,CF+FA=CA,∴AF+EF=DE;
(2)解:(1)中猜想结论不成立,关系式是AF=EF+DE.理由是:
连接BF.在Rt△BEF和Rt△BCF中,∵BC=BE,BF=BF,∴Rt△BEF≌Rt△BCF(HL),∴EF=FC,∵AC=DE,由AF=AC+FC知:AF=DE+EF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|2a+b|与
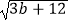 互为相反数.
互为相反数.
(1)求2a﹣3b的平方根;
(2)解关于x的方程ax2+4b﹣2=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中变形正确的是( ) ①4x+8=0变形为x+2=0;
②x+6=5﹣2x变形为3x=﹣1;
③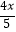 =3变形为4x=15;
=3变形为4x=15;
④4x=2变形为x=2.
A.①④
B.①②③
C.③④
D.①②④ -
科目: 来源: 题型:
查看答案和解析>>【题目】①2﹣
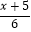 =x﹣
=x﹣ 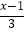 ②3(x﹣2)+1=x﹣(2x﹣1)
②3(x﹣2)+1=x﹣(2x﹣1)
③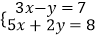 (用代入法)
(用代入法)
④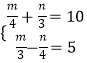 (用加减法)
(用加减法) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC.
(1)证明:BC=DE;
(2)若AC=12,求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(ab2)2·(-a3b)3÷(-4a3b2); (2)
 m(3m2-4m+5)-
m(3m2-4m+5)- m(4m+3);
m(4m+3);(3)(2x+y-3)2; (4)(4x-3y+2)(4x+3y+2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a2﹣3b=6,则4(a2﹣3b)2﹣2a2+6b+4= .
相关试题

