【题目】某校开设武术、舞蹈、剪纸三项活动课程,为了了解学生对这三项活动课程的兴趣情况,随机抽取了部分学生进行调查(每人从中只能选一顶),并将调查结果绘制成下面两幅统计图,请你结合图中信息解答问题.

(1)将条形统计图补充完整;
(2)本次抽样调查的样本容量是 ;
(3)在扇形统计图中,求女生喜欢剪纸活动课程人数对应的圆心角度数;
(4)已知该校有1200名学生,求全校学生中喜欢武术的人数.
参考答案:
【答案】(1)见解析;(2)100;(3)115.2°;(4)480.
【解析】
(1)根据扇形统计图可得出女生喜欢武术的占20%,利用条形图中喜欢武术的女生有10人,即可求出女生总人数,即可得出喜欢舞蹈的人数;
(2)根据(1)的计算结果再利用条形图即可得出样本容量;
(3)360°.以女生中剪纸类人数所占比例即可得;
(4)用全校学生数×喜欢武术的学生在样本中所占比例即可求出.
解:(1)被调查的女生人数为10÷20%=50人,则女生舞蹈类人数为50-(10+16)=24人.
补全图形如:
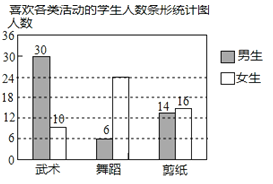
(2)样本容量为50+30+6+14-100,故答案为:100
(3)扇形图中剪纸所占的圆心角度数为360°×![]() =115.2°
=115.2°
故答案为:115.2;
(4)估计全校学生中喜欢剪纸的人数是1200×![]() =480人.
=480人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不透明的袋子中装有大小、质地完全相同的2个白球和2个黑球.
(1) 先从袋中投出1个球后放回,混合均匀后再摸出1个球,则第一次摸到白球,第二次摸到黑球的概率为P1为__________;
(2) 若第一次从袋子中摸出1个球后不放回,第二次再摸出1个球,则两次摸到的球中有1个白球和1个黑球的概率P2是多少?(请用画树形图或列表法求出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1
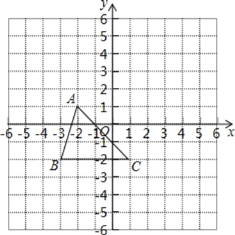
(1)在图中画出△A1B1C1;
(2)点A1,B1,C1的坐标分别为 、 、 ;
(3)若直线BC上有一点P,使△PAC的面积是△ABC面积的2倍,直接写出P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )

A.2.2米B.2.3米C.2.4米D.2.5米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,以AC为边在△ABC外作正△ACD,连接BD.
(1)以点A为中心,把△ADB顺时针旋转60°,画出旋转后的图形(保留作图痕迹);
(2)若∠ABC=30°,BC=4,BD=6,求AB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C= 90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连接EF.
(1)求证:∠1= ∠F;
(2)若CD= 3,EF=
 ,求⊙O的半径长.
,求⊙O的半径长.
-
科目: 来源: 题型:
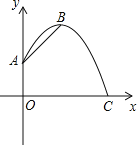
查看答案和解析>>【题目】一自动喷灌设备的喷流情况如图所示,设水管OA在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线与y轴成45°角,水流最高点B比喷头A高2米.
(1)求水流落地点C到O点的距离;
(2)若水流的水平位移s(米)(抛物线上两对称点之间的距离)与水流的运动时间(t秒)之间的函数关系为t= 0.8s,求共有几秒钟,水流高度不低于2米?
相关试题

