Question

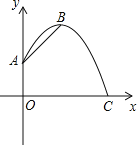
【题目】一自动喷灌设备的喷流情况如图所示，设水管OA在高出地面1.5米的A处有一自动旋转的喷水头，一瞬间流出的水流是抛物线状，喷头A与水流最高点B连线与y轴成45°角，水流最高点B比喷头A高2米．

（1）求水流落地点C到O点的距离；

（2）若水流的水平位移s（米）（抛物线上两对称点之间的距离）与水流的运动时间（t秒）之间的函数关系为t= 0.8s，求共有几秒钟，水流高度不低于2米？

Answer 1

【答案】（1）2+；（2）秒 ．

【解析】试题分析：（1）作BD⊥y轴于点D，由∠DAB=45°，就可以求出AD=BD=2，就可以求出B的坐标，设抛物线的解析式为y=a（x-2）2+3.5，由待定系数法求出其解析式，把y=0时代入解析式求出其解即可；

（2）当y=2时代入（1）的解析式求出x的值，再将x的值代入t=0.8x求出t的值即可．

试题解析：（1）作BD⊥y轴于点D，

∴∠ADB=90°，

∵∠DAB=45°，

∴∠ABD=∠DBA=45°，

∴AD=BD=2，

∴B（2，3.5），

∵OA=1.5，

∴A（0，1.5），

设抛物线的解析式为y=a（x-2）2+3.5，由题意，得

1.5=4a+3.5，

解得：a=-0.5，

∴y=-0.5（x-2）2+3.5，

当y=0时，0=-0.5（x-2）2+3.5，

解得：x1=2+，x2=2-（舍去），

∴水流落地点C到O点的距离为（2+）米；

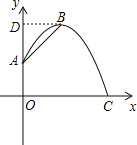
（2）当y=2时，

2=-0.5（x-2）2+3.5．

解得：x1=2+ ，x2=2-，

∴水流位移的距离为：2+-（2-）=2，

∴t=0.8×2=秒

即共有秒钟，水流高度不低于2米．