【题目】已知一条射线OA,若从点O再引两条射线OB和OC,使∠AOB=80°,∠BOC=40°,若OD平分∠AOC,则∠BOD的度数为________.
参考答案:
【答案】60°或20°
【解析】
根据题意可以得到存在两种情况,然后分别画出相应的图形,然后根据图形计算出相应的角的度数,本题得以解决.
由题意可得:分两种情况,
第一种情况如下图一所示,
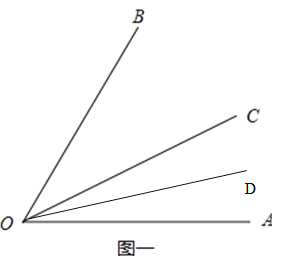
∵∠AOB=80°,∠BOC=40°,∴∠AOC=∠AOB﹣∠BOC=80°﹣40°=40°.∵OD平分∠AOC,∴∠DOC=40°÷2=20°,∴∠BOD=∠BOC+∠DOC=40°+20°=60°.
第二种情况如下图二所示,
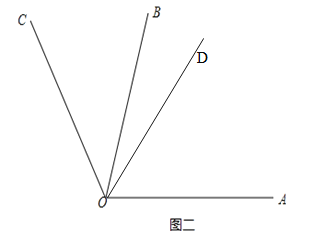
∵∠AOB=80°,∠BOC=40°,∴∠AOC=∠AOB+∠BOC=80°+40°=120°.∵OD平分∠AOC,∴∠DOC=120°÷2=60°,∴∠BOD=∠DOC-∠BOC =60°-40°=20°.
故答案为:60°或20°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB和CD的公共部分BD=
 AB=
AB=  CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E,点F分别在菱形ABCD的边AB,AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若
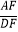 =2,则
=2,则 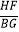 的值为( )
的值为( ) 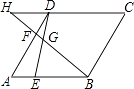
A. ??
??
B.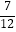 ??
??
C. ??
??
D.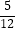
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内部,∠BOE=
 ∠EOC,∠DOE=70°,求∠EOC的度数.
∠EOC,∠DOE=70°,求∠EOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,下列结论:①b<2a;②a+2c﹣b>0;③b>a>c;④b2+2ac<3ab.其中正确结论的个数是( )
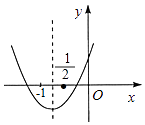
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)992-102×98;
(2)[x(x2y2-xy)-y(x2-x3y)]÷x2y.
【答案】(1)-195(2)2xy-2
【解析】试题分析:(1)利用平方差公式,完全平方公式简便计算.
(2)提取公因式,化简.
试题解析:
(1)原式=(100-1)2-(100+2)×(100-2)
=(1002-200+1)-(1002-4)=-200+5=-195.
(2)原式=[x2y(xy-1)-x2y(1-xy)]÷x2y
=2x2y(xy-1)÷x2y=2(xy-1)=2xy-2.
【题型】解答题
【结束】
21【题目】(1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=
 ;
;(2)若x2-5x=3,求(x-1)(2x-1)-(x+1)2+1的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条直线上任取一点A,截取AB=20 cm,再截取AC=18 cm,M,N分别是AB,AC的中点,求M,N两点之间的距离.
相关试题

