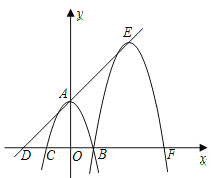
【题目】如图，在平面直角坐标系xoy中，二次函数（）的图象经过A（0，4），B（2，0），C（-2，0）三点．

（1）求二次函数的解析式；

（2）在x轴上有一点D（-4，0），将二次函数图象沿DA方向平移，使图象再次经过点B．

①求平移后图象顶点E的坐标；

②求图象A，B两点间的部分扫过的面积．

参考答案：

【答案】（1）y=-x2+4;(2) E（5，9）；（3）30.

【解析】试题分析： 用待定系数法即可求得二次函数解析式.

①求出直线DA的解析式，设E（m，m+4），根据顶点式写出平移之后的二次函数解析式．把点的坐标代入求出的值，即可求出顶点E的坐标.

②连接AB，过点B作BL∥AD交平移后的抛物线于点G，连结EG，四边形ABGE的面积就是图象A，B两点间的部分扫过的面积．求出四边形的面积即可.

试题解析：

（1）把代入，得

，

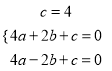解得，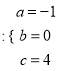

．

（2）①设直线DA的解析式为y=kx+d(k≠0)，

把A（0，4），D（-4，0）代入得，

，

解得： ，

∴y=x+4，

设E（m，m+4），

平移后的抛物线的解析式为： ．

把B（2，0）代入得：

解得： 舍去，

∴E（5，9）．

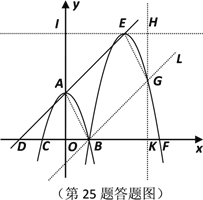
②如图，连接AB，过点B作BL∥AD交平移后的抛物线于点G，连结EG，

∴四边形ABGE的面积就是图象A，B两点间的部分扫过的面积．

过点G作GK⊥x轴于点K，过点E作EI⊥y轴于点I，直线EI，GK交于点H．

由点A（0，4）平移至点E（5，9），可知点B先向右平移5个单位，再向上平移5个单位至点G．

∵B（2，0），∴点G（7，5），

∴GK=5，OB=2，OK=7，

∴BK=OK-OB=7-2=5，

∵A（0,4），E（5,9），

∴AI=9-4=5，EI=5，

∴EH=7-5=2，HG=9-5=4，

∴S四边形ABGH=S矩形IOKH

答：图象A，B两点间的部分扫过的面积为30.

关闭