【题目】如图,在等边△BCD中,DF⊥BC于点F,点A为直线DF上一动点,以B为旋转中心,把BA顺时针方向旋转60°至BE,连接EC.
(1)当点A在线段DF的延长线上时,
①求证:DA=CE;
②判断∠DEC和∠EDC的数量关系,并说明理由;
(2)当∠DEC=45°时,连接AC,求∠BAC的度数.

参考答案:
【答案】(1)①证明见解析②∠DEC+∠EDC=90°;(2)150°或30°
【解析】试题分析: ![]() ①证明△BAD≌△BEC,即可证明.
①证明△BAD≌△BEC,即可证明.
②分别求出![]() 和
和![]() 的度数,即可求出∠DEC和∠EDC的数量关系.
的度数,即可求出∠DEC和∠EDC的数量关系.
![]() 分三种情况进行讨论.
分三种情况进行讨论.
试题解析:
(1)①证明:∵把BA顺时针方向旋转60°至BE,
∴![]() 60°,
60°,

![]() 在等边△BCD中,
在等边△BCD中,
![]() ,
, ![]()
![]() ,
,
![]() ,
,
![]() ,
,
∴△BAD≌△BEC,
∴DA=CE;
②判断:∠DEC+∠EDC=90°.
![]() ,
, ![]() ,
, ![]() ,
,
∵△BAD≌△BEC,
∴∠BCE=∠BDA=30°,
![]() 在等边△BCD中,∠BCD=60°,
在等边△BCD中,∠BCD=60°,
∴∠DCE=∠BCE+∠BCD=90°,∴∠DEC+∠EDC=90°.
(2)分三种情况考虑:
①当点A在线段DF的延长线上时(如图1),
由(1)可得, ![]() 是直角三角形,
是直角三角形, ![]() ,
,
当![]() 时,
时,
![]() ,
,
![]() ,
, ![]() ,
,
由(1)得DA=CE,∴CD=DA,在等边![]() 中,
中, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
,
![]() .
.
②当点A在线段DF上时(如图2),
以B为旋转中心,把BA顺时针旋转![]() 至BE.
至BE.
![]() ,
,

在等边![]() 中,
中, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
在![]()
![]() ,
,
![]() <
<![]() ,
,
∵DA<DF,DA=CE,
∴CE<DC,
由②可知![]() 为直角三角形,
为直角三角形,
∴∠DEC≠45°.
③当点A在线段FD的延长线上时(如图3),

同第②种情况可得![]() ≌
≌![]() ,
,
![]() ,
,
在等边![]() 中,
中, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,
时,
![]() ,
,
![]() ,
,
![]() ,
,
∴AD=CD=BD,
∵![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
综上所述, 的度数是
![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,C,D,B在以O点为圆心,OA长为半径的圆弧上, AC=CD=DB,AB交OC于点E.求证:AE=CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】程大位是我国明朝商人,珠算发明家,他60岁时完成的《直指算法综宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法,书中有如下问题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁,意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,则小和尚有__________人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个有进水管与出水管的容器,从某时刻开始的4分内只进水不出水,在随后的若干分内既进水又出水,之后只有出水不进水,每分钟的进水量和出水量是两个常数,容器内的水量
 (单位:升)与时间
(单位:升)与时间 (单位:分)之间的关系如图所示,则进水速度是______升/分,出水速度是______升/分,
(单位:分)之间的关系如图所示,则进水速度是______升/分,出水速度是______升/分, 的值为______.
的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明、小红和小光共解出了100道数学题目,每人都解出了其中的60道题目,如果将其中只有1人解出的题目叫做难题,2人解出的题目叫做中档题,3人都解出的题目叫做容易题,那么难题比容易题多________道.
-
科目: 来源: 题型:
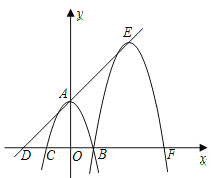
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,二次函数
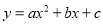 (
(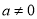 )的图象经过A(0,4),B(2,0),C(-2,0)三点.
)的图象经过A(0,4),B(2,0),C(-2,0)三点.(1)求二次函数的解析式;
(2)在x轴上有一点D(-4,0),将二次函数图象沿DA方向平移,使图象再次经过点B.
①求平移后图象顶点E的坐标;
②求图象A,B两点间的部分扫过的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有三面小旗,分别为红、黄、蓝三种颜色.
⑴.把三面小旗从左到右排列,红色小旗在最左端的概率是多少?
⑵.黄色小旗排在蓝色小旗前的概率是多少?
相关试题

