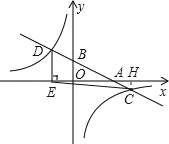
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数![]() 的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(6,﹣1),DE=3.
的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(6,﹣1),DE=3.

(1)求反比例函数与一次函数的解析式;
(2)求△CDE的面积.
参考答案:
【答案】(1)y=﹣![]() ,y=﹣
,y=﹣![]() x+2;(2)12.
x+2;(2)12.
【解析】试题分析: ![]() 分析题意,已知点
分析题意,已知点![]() 在反比例函数的图象上,将
在反比例函数的图象上,将![]() 点坐标代入反比例函数的解析式中即可得到
点坐标代入反比例函数的解析式中即可得到![]() 的值,再由
的值,再由![]() 的长度求出点D的坐标;把
的长度求出点D的坐标;把![]() 两点的坐标代入一次函数即可求得一次函数的解析式.
两点的坐标代入一次函数即可求得一次函数的解析式.
![]() 过C作CH⊥
过C作CH⊥![]() 轴于点H,根据 S△CDE=S△CAE+S△DAE,即可求出面积.
轴于点H,根据 S△CDE=S△CAE+S△DAE,即可求出面积.
试题解析:(1)∵点![]() 在反比例
在反比例![]() 图象上,
图象上,
∴将![]() 代入反比例解析式得:
代入反比例解析式得: ![]() 即
即![]()
∴反比例解析式为![]()
∵点![]() 在反比例函数图象上,且
在反比例函数图象上,且![]() 即
即![]() 纵坐标为3,
纵坐标为3,
将![]() 代入反比例解析式得:
代入反比例解析式得: ![]() 即
即![]()
∴点![]() 坐标为
坐标为![]()
设直线解析式为![]() ,将
,将![]() 与
与![]() 坐标代入得:
坐标代入得: ![]()
解得: 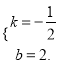
∴一次函数解析式为![]()
(2)过C作CH⊥![]() 轴于点H,
轴于点H,
![]()
对于一次函数![]() 令
令![]() 求得
求得![]() ,故
,故![]()
由![]() 坐标
坐标![]() 得到
得到![]()
![]()
∴S△CDE=S△CAE+S△DAE![]()
-
科目: 来源: 题型:
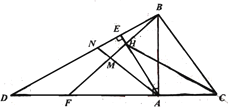
查看答案和解析>>【题目】如图,已知
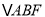 为等腰直角三角形,
为等腰直角三角形,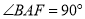 ,
, 、
、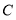 为直线
为直线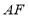 上两点,且满足
上两点,且满足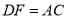 ,连接
,连接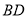 、
、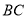 ,过点
,过点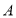 作
作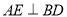 于点
于点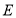 ,交
,交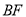 于点
于点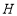 ,连接
,连接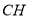 .
.
(1)若
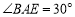 ,
,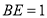 ,求
,求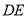 的长;
的长;(2)若点
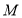 是线段
是线段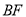 上的动点,连
上的动点,连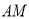 并延长交
并延长交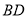 于
于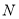 ,当
,当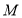 在线段
在线段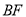 的什么位置上时,
的什么位置上时,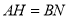 ?请说明理由;
?请说明理由;(3)在(2)的结论下,判断线段
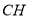 、
、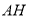 、
、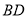 的数量关系.请说明理由.
的数量关系.请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P有_____个.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△MNP中,∠P=60°,MN=NP,MQ⊥PN,垂足为Q,延长MN至点G,取NG=NQ,若△MNP的周长为12,MQ=a,则△MGQ周长是 ( )

A.8+2aB.8aC.6+aD.6+2a
-
科目: 来源: 题型:
查看答案和解析>>【题目】D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由.)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=∠ACB,AD、BD分别平分△ABC的外角∠EAC、内角∠ABC,以下结论:① AD∥BC;②∠ACB=2∠ADB;③ BD⊥AC;④ AC=AD.其中正确的结论有( )

A.①②B.①②④C.①②③D.①③④
相关试题

