【题目】如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P有_____个.

参考答案:
【答案】4
【解析】
由A点坐标可得OA=2![]() ,∠AOP=45°,分别讨论OA为腰和底边,求出点P在x轴正半轴和负半轴时,△APO是等腰三角形的P点坐标即可.
,∠AOP=45°,分别讨论OA为腰和底边,求出点P在x轴正半轴和负半轴时,△APO是等腰三角形的P点坐标即可.
(1)当点P在x轴正半轴上,
①如图,以OA为腰时,
∵A的坐标是(2,2),
∴∠AOP=45°,OA=2![]() ,
,
当∠AOP为顶角时,OA=OP=2![]() ,
,
当∠OAP为顶角时,AO=AP,
∴OPA=∠AOP=45°,
∴∠OAP=90°,
∴OP=![]() OA=4,
OA=4,
∴P的坐标是(4,0)或(2![]() ,0).
,0).
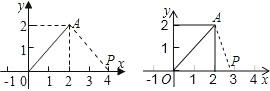
②以OA为底边时,
∵点A的坐标是(2,2),
∴∠AOP=45°,
∵AP=OP,
∴∠OAP=∠AOP=45°,
∴∠OPA=90°,
∴OP=2,
∴P点坐标为(2,0).
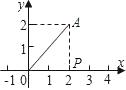
(2)当点P在x轴负半轴上,
③以OA为腰时,
∵A的坐标是(2,2),
∴OA=2![]() ,
,
∴OA=OP=2![]() ,
,
∴P的坐标是(﹣2![]() ,0).
,0).

综上所述:P的坐标是(2,0)或(4,0)或(2![]() ,0)或(﹣2
,0)或(﹣2![]() ,0).
,0).
故答案为:4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】喜迎新中国70华诞,感受祖国70年沧桑巨变,70年壮丽辉煌,西大附中开展“祖国,我为你骄傲”的歌唱比赛,为了筹集歌唱比赛的演出服装资金,初二年级从批发市场购进
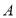 、
、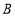 两种材料用于手工制作,进行“爱心义卖”.若每个
两种材料用于手工制作,进行“爱心义卖”.若每个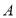 种材料的进价比每个
种材料的进价比每个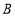 种材料的进价少2元,且用160元购进
种材料的进价少2元,且用160元购进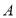 种材料的数量与用200元购进
种材料的数量与用200元购进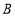 种材料的数量相等.
种材料的数量相等.(1)求
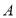 、
、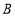 两种材料的进价分别为多少元?
两种材料的进价分别为多少元?(2)同学们齐心协力、大胆创新制作出了新颖别致的甲、乙两种手工艺品共56个,乙的数量比甲的数量的两倍还多,但多的个数不超过2个,甲的售价是24元/个,乙的售价是30元/个,为了使利润不低于1040元,有几种制作方案,哪种利润方案最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
-
科目: 来源: 题型:
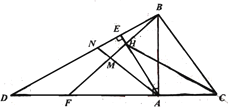
查看答案和解析>>【题目】如图,已知
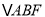 为等腰直角三角形,
为等腰直角三角形,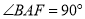 ,
, 、
、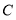 为直线
为直线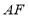 上两点,且满足
上两点,且满足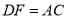 ,连接
,连接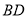 、
、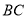 ,过点
,过点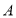 作
作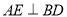 于点
于点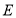 ,交
,交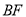 于点
于点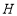 ,连接
,连接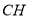 .
.
(1)若
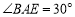 ,
,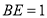 ,求
,求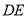 的长;
的长;(2)若点
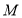 是线段
是线段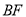 上的动点,连
上的动点,连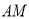 并延长交
并延长交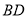 于
于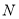 ,当
,当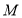 在线段
在线段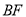 的什么位置上时,
的什么位置上时,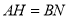 ?请说明理由;
?请说明理由;(3)在(2)的结论下,判断线段
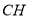 、
、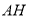 、
、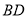 的数量关系.请说明理由.
的数量关系.请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△MNP中,∠P=60°,MN=NP,MQ⊥PN,垂足为Q,延长MN至点G,取NG=NQ,若△MNP的周长为12,MQ=a,则△MGQ周长是 ( )

A.8+2aB.8aC.6+aD.6+2a
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数
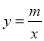 的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(6,﹣1),DE=3.
的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(6,﹣1),DE=3.
(1)求反比例函数与一次函数的解析式;
(2)求△CDE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由.)

相关试题

