【题目】如图,![]() ,且
,且![]() ,
,![]() ,且
,且![]() ,请按照图中所标注的数据计算图中实线所围成的图形的面积
,请按照图中所标注的数据计算图中实线所围成的图形的面积![]() ______.
______.

参考答案:
【答案】50
【解析】
根据∠F=∠AGB=∠EAB=90°,证明∠FEA=∠BAG,再根据AAS证△FEA≌△GAB,推出AG=EF=6,AF=BG=2,同理CG=DH=4,BG=CH=2,求出FH=14,根据阴影部分的面积=S梯形EFHD-S△EFA-S△ABC-S△DHC和面积公式代入求出即可.
∵AE⊥AB,EF⊥AF,BG⊥AG,
∴∠F=∠AGB=∠EAB=90°,
∴∠FEA+∠EAF=90°,∠EAF+∠BAG=90°,
∴∠FEA=∠BAG,
在△FEA和△GAB中,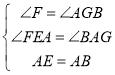 ,
,
∴△FEA≌△GAB(AAS),
∴AG=EF=6,AF=BG=2,
同理可证:△CBG≌△DCH(AAS),
∴CG=DH=4,BG=CH=2,
∴FH=2+6+4+2=14,
∴梯形EFHD的面积=![]() ×(EF+DH)×FH=
×(EF+DH)×FH=![]() ×(6+4)×14=70,
×(6+4)×14=70,
∴阴影部分的面积=S梯形EFHDS△EFAS△ABCS△DHC
=70![]() ×6×2
×6×2![]() ×(6+4)×2
×(6+4)×2![]() ×4×2
×4×2
=50.
故答案为50.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=∠ACB。

(1)若D为BC边上一点,E为直线AC上一点,且∠ADE=∠AED.求证:∠BAD=2∠CDE;
(2)如图,若D在BC的反向延长线上,其它条件不变,(1)中的结论是否仍然成立?证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
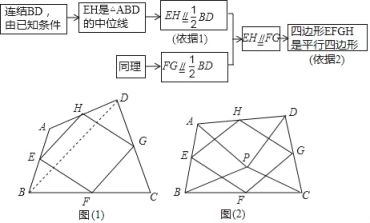
问题情境:在数学活动课上,我们给出如下定义:顺次连按任意一个四边形各边中点所得的四边形叫中点四边形.如图(1),在四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.试说明中点四边形EFGH是平行四边形.
探究展示:勤奋小组的解题思路:
反思交流:
(1)①上述解题思路中的“依据1”、“依据2”分别是什么?
依据1: ;依据2: ;
②连接AC,若AC=BD时,则中点四边形EFGH的形状为 ;
创新小组受到勤奋小组的启发,继续探究:
(2)如图(2),点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并说明理由;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其它条件不变,则中点四边形EFGH的形状为 .
-
科目: 来源: 题型:
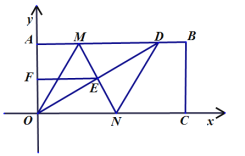
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知矩形AOCB的顶点O、A的坐标分别是(0,0)、(0,a),且满足
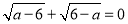 . 点D是AB上一点, M,N垂直平分OD,分别交AB,OD,OC于点M,E,N,连接OM,DN.
. 点D是AB上一点, M,N垂直平分OD,分别交AB,OD,OC于点M,E,N,连接OM,DN.(1)填空:a = ;
(2)求证:四边形MOND是菱形;
(3)若F为OA的中点,连接EF,且满足EF+OE=9,求四边形MOND的周长和面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC≌△ADE,BC的延长线交AD于点M,交DE于点F.若∠D=25°,∠AED=105°,∠DAC=10°,求∠DFB的度数.
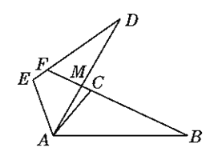
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是面积为
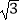 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于(结果保留根号).
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于(结果保留根号). 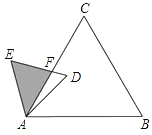
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了增强学生对中华优秀传统文化的理解,决定购买一批相关的书籍.据了解,经典著作的单价比传说故事的单价多6元,用10000元购买经典著作与用7000元购买传说故事的本数相同,这两类书籍的单价各是多少元?
相关试题

