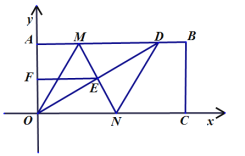
【题目】如图,在平面直角坐标系中,已知矩形AOCB的顶点O、A的坐标分别是(0,0)、(0,a),且满足![]() . 点D是AB上一点, M,N垂直平分OD,分别交AB,OD,OC于点M,E,N,连接OM,DN.
. 点D是AB上一点, M,N垂直平分OD,分别交AB,OD,OC于点M,E,N,连接OM,DN.
(1)填空:a = ;
(2)求证:四边形MOND是菱形;
(3)若F为OA的中点,连接EF,且满足EF+OE=9,求四边形MOND的周长和面积.
参考答案:
【答案】(1)6;(2)详见解析;(3)C菱形MOND=25,S菱形MOND=![]()
【解析】
(1)根据二次根式的非负性进行求解即可;
(2)根据矩形AOCB的性质以及![]() 判定四边形MOND是平行四边形,再由菱形的判定求证即可;
判定四边形MOND是平行四边形,再由菱形的判定求证即可;
(3)根据![]() 的中位线及矩形AOCB的性质构造直角三角形,设AD=x,
的中位线及矩形AOCB的性质构造直角三角形,设AD=x,![]()
利用勾股定理求出x的值,再根据菱形MOND的性质,设![]() ,
,![]() ,利用勾股定理求出y,最后根据菱形的周长及面积求法进行求解即可.
,利用勾股定理求出y,最后根据菱形的周长及面积求法进行求解即可.
(1)∵![]()
∴![]() ,
,![]()
∴![]()
∴![]() ;
;
(2)证明:∵MN垂直平分OD
∴OM=DM,DE=OE,![]()
∵四边形AOCB是矩形
∴AB∥OC
∴![]()
在![]() 和
和![]() 中
中
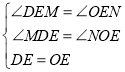
∴![]()
∴ME=NE
又∵DE=OE
∴四边形MOND是平行四边形
又∵OM=DM
∴四边形MOND是菱形;
(3)由(1)得OA=6
由(2)得DE=OE
又∵F为OA的中点
∴EF是![]() 的中位线,
的中位线,
∴![]()
又∵EF+OE=9,DE=OE
∴![]()
∴AD+OD =18
∵四边形AOCB是矩形
∴![]()
在![]() 中
中
设AD=x,则![]()
根据勾股定理,![]() ,解得x=8
,解得x=8
∴AD=8,OD =10
由(2)得,四边形MOND是菱形
∴OM=MD=DN=ON
设![]() ,则
,则![]()
在![]() 中,根据勾股定理
中,根据勾股定理
![]() ,解得
,解得![]()
∴![]()
∴![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,大正方形的边长为4厘米,小正方形的边长为2厘米,状态如图所示。大正方形固定不动,把小正方形以1厘米∕秒的速度向大正方形的内部沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S厘米2,完成下列问题:

(1)平移到1.5秒时,重叠部分的面积为 厘米2.
(2)求小正方形在平移过程中,S与t的关系式。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=∠ACB。

(1)若D为BC边上一点,E为直线AC上一点,且∠ADE=∠AED.求证:∠BAD=2∠CDE;
(2)如图,若D在BC的反向延长线上,其它条件不变,(1)中的结论是否仍然成立?证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
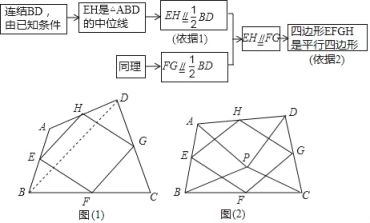
问题情境:在数学活动课上,我们给出如下定义:顺次连按任意一个四边形各边中点所得的四边形叫中点四边形.如图(1),在四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.试说明中点四边形EFGH是平行四边形.
探究展示:勤奋小组的解题思路:
反思交流:
(1)①上述解题思路中的“依据1”、“依据2”分别是什么?
依据1: ;依据2: ;
②连接AC,若AC=BD时,则中点四边形EFGH的形状为 ;
创新小组受到勤奋小组的启发,继续探究:
(2)如图(2),点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并说明理由;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其它条件不变,则中点四边形EFGH的形状为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,且
,且 ,
, ,且
,且 ,请按照图中所标注的数据计算图中实线所围成的图形的面积
,请按照图中所标注的数据计算图中实线所围成的图形的面积 ______.
______.
-
科目: 来源: 题型:
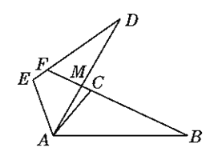
查看答案和解析>>【题目】如图,已知△ABC≌△ADE,BC的延长线交AD于点M,交DE于点F.若∠D=25°,∠AED=105°,∠DAC=10°,求∠DFB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是面积为
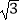 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于(结果保留根号).
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于(结果保留根号). 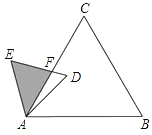
相关试题

