搜索
【题目】对于实数a，b，定义运算“◎”如下：a◎b＝（a +b）2﹣（a﹣b）2．
例如：3◎2＝（3 +2）2﹣（3﹣2）2 若（m +2）◎（m﹣3）＝24，求m的值．
参考答案：
【答案】﹣3或4．
【解析】
利用新定义得到[（m+2）+（m﹣3）]2﹣[（m+2）﹣（m﹣3）]2＝24，整理得到（2m1）249＝0，然后利用因式分解法解方程．
解：根据题意得[（m+2）+（m﹣3）]2﹣[（m+2）﹣（m﹣3）]2＝24，
（2m﹣1）2﹣49＝0，
（2m﹣1+7）（2m﹣1﹣7）＝0，
2m﹣1+7＝0或2m﹣1﹣7＝0，
所以m1＝﹣3，m2＝4．
故答案为﹣3或4．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若x＜y，且(a－3)x＞(a－3)y，则a的取值范围是________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，对角线AC平分∠BAD，AB＞AD，下列结论中正确的是（ ）
A.AB﹣AD＞CB﹣CD
B.AB﹣AD=CB﹣CD
C.AB﹣AD＜CB﹣CD
D.AB﹣AD与CB﹣CD的大小关系不确定 -
科目： 来源： 题型：
查看答案和解析>>【题目】若x2+mx+16是一个完全平方式，则m的取值是（ ）
A. 8 B. ﹣8 C. ±8 D. ±4
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知四边形ABCD中，对角线BD平分∠ABC，∠ACB=72°，∠ABC=50°，并且∠BAD+∠CAD=180°，那么∠ADC的度数为（ ）
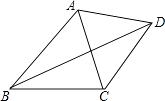
A.62°
B.65°
C.68°
D.70° -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1 ．
（1）当∠A为70°时， ∵∠ACD﹣∠ABD=∠
∴∠ACD﹣∠ABD=°
∵BA1、CA1是∠ABC的角平分线与∠ACB的外角∠ACD的平分线
∴∠A1CD﹣∠A1BD=
（∠ACD﹣∠ABD）
∴∠A1=°；
（2）∠A1BC的角平分线与∠A1CD的角平分线交于A2 ， ∠A2BC与A2CD的平分线交于A3 ， 如此继续下去可得A4、…、An ， 请写出∠A与∠An的数量关系；
（3）如图2，四边形ABCD中，∠F为∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的角，若∠A+∠D=230度，则∠F= ．
（4）如图3，若E为BA延长线上一动点，连EC，∠AEC与∠ACE的角平分线交于Q，当E滑动时有下面两个结论：①∠Q+∠A1的值为定值；②∠Q﹣∠A1的值为定值．其中有且只有一个是正确的，请写出正确的结论，并求出其值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如果a=（﹣
）2、b=（﹣2014）0、c=（﹣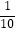 
）﹣1 ， 那么a、b、c的大小关系为（ ）
A.a＞b＞c
B.a＞c＞b
C.c＞b＞a
D.c＞a＞b
相关试题
