【题目】如图,ABCD中,E、F分别是AD,BC的中点.求证:(1)△AFB≌△CED;(2)四边形AECF是平行四边形.

参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)利用平行四边形的性质结合全等三角形的判定方法得出即可;
(2)利用一组对边平行且相等的四边形是平行四边形进而得出即可.
证明:(1)∵四边形ABCD是平行四边形,
∴AB=DC,∠B=∠D,AD=BC,
∵E、F分别是AD,BC的中点,
∴AE=DE=FC=BF,
在△AFB和△CED中,
AB=DC,∠B=∠D,BF=DE,
∴△AFB≌△CED(SAS);
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,
又∵AE=CF,
∴四边形AECF是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有若干根长度相同的火柴棒,用a根火柴棒,按如图①摆放时可摆成m个正方形,用b根火柴棒,按如图②摆放时可摆成2n个正方形.(m、n是正整数)

(1)如图①,当m=4时,a=______;如图②,当b=52时,n=______;
(2)当若干根长度相同的火柴棒,既可以摆成图①的形状,也可以摆成图②的形状时,m与n之间有何数量关系,请你写出来并说明理由;
(3)现有61根火柴棒,用若干根火柴棒摆成图①的形状后,剩下的火柴棒刚好可以摆成图②的形状.请你直接写出一种摆放方法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】李明同学早上骑自行车上学,中途因道路施工需步行一段路,到学校共用时18分钟,他骑自行车的平均速度是300米/分钟,步行的平均速度是120米/分钟,他家离学校的距离是4500米.
(1)李明上学时骑自行车的路程和步行的路程分别为多少米?
(2)放学后李明从17:40开始离校回家,但此时道路施工的地段增长了600米,如果按照上学时的速度,问李明能否在18:00之前到家?请通过计算说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=y1+y2,y1与x成正比例,y2与x-2成正比例,当x=1时,y=0;当x=-3时,y=4.
(1)求y与x的函数关系式,并说明此函数是什么函数;
(2)当x=3时,求y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上的A,B,C三点所表示的数分别为a,b,c,其中AB=BC.如果
 ,那么该数轴的原点O的位置应该在( )
,那么该数轴的原点O的位置应该在( )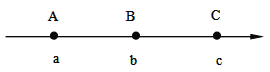
A.点A的左边
B.点A与点B之间
C.点B与点C之间(靠近点B)
D.点C的右边
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=6,∠BAD的平分线与BC的延长线交于点E、与DC交于点F,且点F为边DC的中点,∠ADC的平分线交AB于点M,交AE于点N,连接DE
(1) 求证:BC=CE
(2) 若DM=2,求DE的长

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一次函数y=﹣x+b的图象与x轴、y轴的交点分别为A、B与反比例函数
 的图象交于点C、D,且
的图象交于点C、D,且 .
.(1)求∠BAO的度数;
(2)求O到DC的距离.

相关试题

