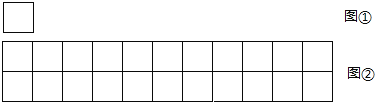
【题目】现有若干根长度相同的火柴棒,用a根火柴棒,按如图①摆放时可摆成m个正方形,用b根火柴棒,按如图②摆放时可摆成2n个正方形.(m、n是正整数)

(1)如图①,当m=4时,a=______;如图②,当b=52时,n=______;
(2)当若干根长度相同的火柴棒,既可以摆成图①的形状,也可以摆成图②的形状时,m与n之间有何数量关系,请你写出来并说明理由;
(3)现有61根火柴棒,用若干根火柴棒摆成图①的形状后,剩下的火柴棒刚好可以摆成图②的形状.请你直接写出一种摆放方法.
参考答案:
【答案】(1)a=13,n=10;(2)3m+1=5n+2;(3)如图①摆放1个正方形,如图②摆放11个正方形
【解析】
(1)根据每多一个正方形多用2根火柴棒写出摆放m个正方形所用的火柴棒的根数,然后把m=4代入进行计算即可得解;
(2)根据a相等列出关于m、n的关系式;
(3)可以摆出图①说明a是比3的倍数多1的数,可以摆出图②说明2a是比5的倍数多2的数,所以,2a取5与6的倍数大2的数,并且现有61根火柴棒进而得出答案.
(1)由图可知,图①每多1个正方形,多用3根火柴棒,所以,m个小正方形共用3m+1根火柴棒,
图②每多2个正方形,多用5根火柴棒,所以,2n个小正方形共用5n+2根火柴棒,
当m=4时,a=3×4+1=13,
图②可以摆放5n+2=52个小正方形,
∴n=10.(2)∵都用a根火柴棒,
∴3m+1=5n+2,
整理得,3m=5n+1;
(3)∵3m+1+5n+2=61,
∴3m+5n=58,
当m=1,n=11,是方程的根,
∴第一个图形摆放3×1+1=4根火柴棒,
第二个图形摆放5×11+2=57根火柴棒,
如图,
∵4+57=61,
∴符合题意(答案不唯一).
-
科目: 来源: 题型:
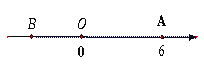
查看答案和解析>>【题目】如图,已知数轴上的点A对应的数为6,B是数轴上的一点,且AB=10,动点P从点A出发,以每秒6个单位长度的速度沿着数轴向左匀速运动,设运动时间为t秒(t>0).
(1)数轴上点B对应的数是_______,点P对应的数是_______(用t的式子表示);
(2)动点Q从点B与点P同时出发,以每秒4个单位长度的速度沿着数轴向左匀速运动,试问:运动多少时间点P可以追上点Q?
(3)M是AP的中点,N是PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若有变化,说明理由;若没有变化,请你画出图形,并求出MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形纸片ABCD中,AB=6 cm,BC=8 cm,点E是BC边上一点,连接AE,并将△AEB沿AE折叠,得到△AEB′,以C,E,B′为顶点的三角形是直角三角形时,BE的长为____cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示:有边长为a的正方形A类卡片、边长为b的正方形B类卡片、长和宽分别为a、b的长方形C类卡片各若干张,如果要拼一个边长分别为
 、
、 的大长方形(不重叠无缝隙),那么需要A类卡片______张,B类卡片_______张,C类卡片______张,并请画出一种拼法.(每类卡片至少使用一张,并在画图时标注好每类卡片的类型及边长 )
的大长方形(不重叠无缝隙),那么需要A类卡片______张,B类卡片_______张,C类卡片______张,并请画出一种拼法.(每类卡片至少使用一张,并在画图时标注好每类卡片的类型及边长 )
-
科目: 来源: 题型:
查看答案和解析>>【题目】李明同学早上骑自行车上学,中途因道路施工需步行一段路,到学校共用时18分钟,他骑自行车的平均速度是300米/分钟,步行的平均速度是120米/分钟,他家离学校的距离是4500米.
(1)李明上学时骑自行车的路程和步行的路程分别为多少米?
(2)放学后李明从17:40开始离校回家,但此时道路施工的地段增长了600米,如果按照上学时的速度,问李明能否在18:00之前到家?请通过计算说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=y1+y2,y1与x成正比例,y2与x-2成正比例,当x=1时,y=0;当x=-3时,y=4.
(1)求y与x的函数关系式,并说明此函数是什么函数;
(2)当x=3时,求y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,E、F分别是AD,BC的中点.求证:(1)△AFB≌△CED;(2)四边形AECF是平行四边形.

相关试题

