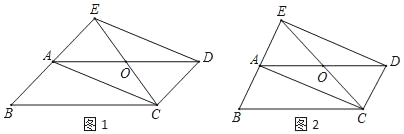
【题目】已知:在平行四边形ABCD中,点O是边AD的中点,连接CO并延长交BA延长线于点E,连接ED、AC.
(1)如图1,求证:四边形AEDC是平行四边形;
(2)如图2,若四边形AEDC是矩形,请探究∠COD与∠B的数量关系,写出你的探究结论,并加以证明.
参考答案:
【答案】(1)见解析;(2)∠COD=180°﹣2∠B,理由见解析
【解析】
(1)由AAS证明△AEO≌△DCO,得出AE=CD,即可得出结论;
(2)由平行四边形的性质得出∠B=∠ADC,根据四边形AEDC是矩形得到AO=EO=CO=DO,求出∠ADC=∠OCD,根据三角形的内角和∠ADC+∠OCD+∠COD=180°,即可得出∠COD与∠B的数量关系.
证明:(1)∵四边形ABCD是平行四边形
∴AB∥CD
∴∠BEC=∠DCE
∵点O是边AD的中点
∴AO=DO,且∠BEC=∠DCE,∠AOE=∠DOC
∴△AEO≌△DCO(AAS)
∴AE=CD
∵AE∥DC,AE=CD
∴四边形AEDC是平行四边形
(2)∠COD=180°﹣2∠B
理由如下:
∵四边形ABCD是平行四边形
∴∠B=∠ADC
∵四边形AEDC是矩形
∴AO=EO=CO=DO
∴∠ADC=∠OCD
∵∠ADC+∠OCD+∠COD=180°
∴∠COD=180°﹣2∠ADC=180°﹣2∠B
-
科目: 来源: 题型:
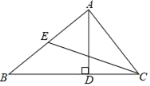
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,垂足为点D,CE是边AB上的中线,如果CD=BE,∠B=40°,那么∠BCE=_____度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两座城市的中心火车站A,B两站相距360 km.一列动车与一列特快列车分别从A,B两站同时出发相向而行,动车的平均速度比特快列车快54 km/h,当动车到达B站时,特快列车恰好到达距离A站135 km处的C站.求动车和特快列车的平均速度各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:通过小学的学习我们知道,分数可分为“真分数”和“假分数”,而假分数都可化为常分数,如:
 =
= 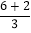 =2+
=2+  =2
=2  .我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.如
.我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.如 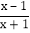 ,
,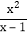 这样的分式就是假分式;再如:
这样的分式就是假分式;再如: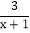 ,
,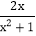 这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).如:
这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).如: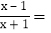
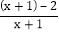 =1-
=1-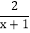 ;
; 解决下列问题:
(1)分式
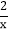 是 分式(填“真分式”或“假分式”);
是 分式(填“真分式”或“假分式”);(2)
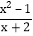 将假分式化为带分式;
将假分式化为带分式;(3)如果 x 为整数,分式
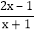 的值为整数,求所有符合条件的 x 的值.
的值为整数,求所有符合条件的 x 的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:OA⊥OC,∠AOB:∠AOC=2:3,画出图形,并求∠BOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,点O是对角线AC的中点,点M为BC上一点,连接AM,且AB=AM,点E为BM中点,AF⊥AB,连接EF,延长FO交AB于点N.
(1)若BM=4,MC=3,AC=
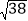 ,求AM的长度;
,求AM的长度;(2)若∠ACB=45°,求证:AN+AF=
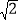 EF.
EF.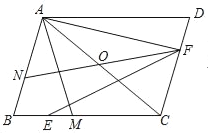
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.△ABC中,∠C=2∠B,D是BC上一点,且AD⊥AB,点E是BD的中点,连结AE.
(1)求证:BD=2AC;
(2)若AE=6.5,AD=5,那么△ABE的周长是多少?
相关试题

