【题目】如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F, 
DE与AB相交于点E.
(1)求证:ABAF=CBCD;
(2)已知AB=15cm,BC=9cm,P是线段DE上的动点.设DP=x cm,梯形BCDP的面积为y ![]() .
.
①求y关于x的函数关系式.
②y是否存在最大值?若有求出这个最大值,若不存在请说明理由.
参考答案:
【答案】
(1)证明:∵AD=CD,DE⊥AC,
∴DE垂直平分AC,
∴AF=CF,∠DFA=∠DFC=90°,∠DAF=∠DCF.
∵∠DAB=∠DAF+∠CAB=90°,∠CAB+∠B=90°,
∴∠DCF=∠DAF=∠B.
在Rt△DCF和Rt△ABC中,∠DFC=∠ACB=90°,∠DCF=∠B,
∴△DCF∽△ABC.
∴ ![]() ,即
,即 ![]() ,
,
∴ABAF=CBCD;
(2)解:连接PB, 
①∵AB=15,BC=9,∠ACB=90°,
∴AC= ![]() =12,
=12,
∴CF=AF=6.
∴y= ![]() (x+9)×6=3x+27;
(x+9)×6=3x+27;
②由EF∥BC,得△AEF∽△ABC.
AE=BE= ![]() AB=
AB= ![]() ,EF=
,EF= ![]() .
.
由∠EAD=∠AFE=90°,∠AEF=∠DEA,得△AEF∽△DEA.
Rt△ADF中,AD=CD= ![]() =10,AF=6,
=10,AF=6,
∴DF=8.
∴DE=DF+FE=8+ ![]() =
= ![]() .
.
∵y=3x+27(0≤x≤ ![]() ),函数值y随着x的增大而增大,
),函数值y随着x的增大而增大,
∴当x= ![]() 时,y有最大值,此时y=
时,y有最大值,此时y= ![]() .
.
【解析】(1)首先判断出DE垂直平分AC,然后根据中垂线的性质及等边对等角得出AF=CF,∠DFA=∠DFC=90°,∠DAF=∠DCF,然后根据同角的余角相等得出∠DCF=∠DAF=∠B,进而判断出△DCF∽△ABC,根据相似三角形对应边成比例得出结论;
(2)连接PB,①根据勾股定理算出AC,进而得出CF=AF=6,然后根据梯形的面积公式得出y关于x的函数关系式;②由EF∥BC,得△AEF∽△ABC.由相似三角形对应边成比例得出AE,BE,EF的长,然后再判断出△AEF∽△DEA,根据相似三角形的性质得出DF的长,进而得出DE=DF+FE,最后根据一次函数的性质得出结论。
【考点精析】认真审题,首先需要了解线段垂直平分线的判定(和一条线段两个端点距离相等的点,在这条线段的垂直平分线上),还要掌握线段垂直平分线的性质(垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
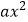 +bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3).
+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3).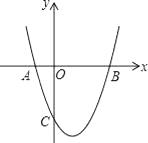
(1)求抛物线的解析式;
(2)D是y轴正半轴上的点,OD=3,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,
①试说明EF是圆的直径;
②判断△AEF的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成推理过程
(1)如图,已知∠1=∠2,∠B=∠C,求证:AB∥CD.
证明∵∠1=∠2(已知),
且∠1=∠CGD( )
∴∠2=∠CGD( ),
∴CE∥BF( ),
∴∠C=∠BFD( )
又∵∠B=∠C(已知),
∴∠BFD=∠B( ),
∴AB∥CD( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】公司投资750万元,成功研制出一种市场需求量较大的产品,并再投入资金1750万元进行相关生产设备的改进.已知生产过程中,每件产品的成本为60元.在销售过程中发现,当销售单价定为120元时,年销售量为24万件;销售单价每增加10元,年销售量将减少1万件.设销售单价为x(元)(x>120),年销售量为y(万件),第一年年获利(年获利=年销售额﹣生产成本)为z(万元).
(1)求出y与x之间,z与x之间的函数关系式;
(2)该公司能否在第一年收回投资. -
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两地相距100千米,甲,乙两人骑车分别从A,B两地相向而行,图中
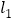 和
和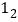 分别表示他们各自到A地的距离
分别表示他们各自到A地的距离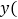 千米
千米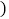 与时间
与时间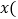 小时
小时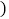 的关系,根据图中提供的信息,解答下列问题:
的关系,根据图中提供的信息,解答下列问题: 图中哪条线表示甲到A地的距离与时间的关系?
图中哪条线表示甲到A地的距离与时间的关系? 甲,乙两人的速度分别是多少?
甲,乙两人的速度分别是多少? 求P点的坐标,并解释P点的实际意义.
求P点的坐标,并解释P点的实际意义. 甲出发多长时间后,两人相距30千米?
甲出发多长时间后,两人相距30千米?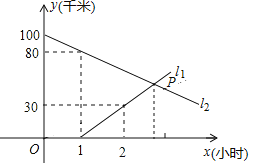
-
科目: 来源: 题型:
查看答案和解析>>【题目】(一)问题提出:如何把n个边长为1的正方形,剪拼成一个大正方形?
(二)解决方法
探究一:若n是完全平方数,我们不用剪切小正方形,可直接将小正方形拼成一个大正方形,如图(1),用四个边长为1的小正方形可以拼成一个大正方形.
问题1:请用9个边长为1的小正方形在图(2)的位置拼成一个大正方形.
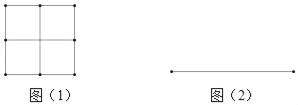
探究二:若n=2,5,10,13等这些数,都可以用两个正整数的平方和来表示,以n=5为例,用5个边长为1的小正方形剪拼成一个大正方形.
(1)计算:拼成的大正方形的面积为5,边长为
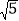 ,可表示成
,可表示成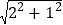 ;
;(2)剪切:如图(3)将5个小正方形按如图所示分成5部分,虚线为剪切线;
(3)拼图:以图(3)中的虚线为边,拼成一个边长为
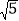 的大正方形,如图(4).
的大正方形,如图(4).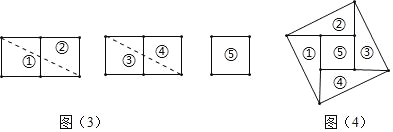
问题2:请仿照上面的研究方式,用13个边长为1的小正方形剪拼成一个大正方形;
(1)计算:拼成的大正方形的面积为____,边长为_____,可表示成____;
(2)剪切:请仿照图(3)的方法,在图(5)的位置画出图形.
(3)拼图:请仿照图(4)的方法,在图(6)的位置出拼成的图.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某射击队有甲、乙两名射手,他们各自射击7次,射中靶的环数记录如下:
甲:8,8,8,9,6,8,9
乙:10,7,8,8,5,10,8
(1)分别求出甲、乙两名射手打靶环数的平均数、众数、中位数;
(2)如果要选择一名成绩比较稳定的射手,代表射击队参加比赛,应如何选择?为什么?
相关试题

