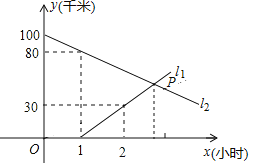
【题目】A,B两地相距100千米,甲,乙两人骑车分别从A,B两地相向而行,图中![]() 和
和![]() 分别表示他们各自到A地的距离
分别表示他们各自到A地的距离![]() 千米
千米![]() 与时间
与时间![]() 小时
小时![]() 的关系,根据图中提供的信息,解答下列问题:
的关系,根据图中提供的信息,解答下列问题:
![]() 图中哪条线表示甲到A地的距离与时间的关系?
图中哪条线表示甲到A地的距离与时间的关系?
![]() 甲,乙两人的速度分别是多少?
甲,乙两人的速度分别是多少?
![]() 求P点的坐标,并解释P点的实际意义.
求P点的坐标,并解释P点的实际意义.
![]() 甲出发多长时间后,两人相距30千米?
甲出发多长时间后,两人相距30千米?
参考答案:
【答案】(1)![]() ;(2) 甲:20千米
;(2) 甲:20千米![]() 时,乙:35千米
时,乙:35千米![]() 时; (3)见解析;(4)
时; (3)见解析;(4)![]() 小时或
小时或![]() 小时.
小时.
【解析】
(1)根据A,B两地相距100千米,甲,乙两人骑车分别从A,B两地相向而行,可知l2表示甲到A地的距离与时间的关系;
(2)根据路程、时间与速度的关系解答即可;
(3)利用待定系数法求出直线l1、l2的解析式,利用两函数相等进而求出相遇的时间;
(4)根据路程、时间与速度的关系列方程解答即可.
(1)由A,B两地相距100千米,甲,乙两人骑车分别从A,B两地相向而行,可知l2表示甲到A地的距离与时间的关系;
(2)甲的速度为:100﹣80=20(千米/时);
乙的速度为:![]() (千米/时);
(千米/时);
(3)设l1的解析式为y=k1x+b1,根据题意得:![]() ,解得:
,解得:![]() ,故l1的解析式为y=30x﹣30;
,故l1的解析式为y=30x﹣30;
设l2的解析式为y=k2x+b2,根据题意得:![]() ,解得:
,解得:![]() ,故l2的解析式为y=﹣20x+100.
,故l2的解析式为y=﹣20x+100.
![]() ,解得:
,解得: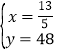 ,所以P点的坐标为
,所以P点的坐标为![]() ,即出发2.6小时后两人相遇,这时两人距离A地48千米;
,即出发2.6小时后两人相遇,这时两人距离A地48千米;
(4)设甲出发x小时,两人相距30千米,根据题意得:
(20+35)x=100﹣30或(20+35)x=100+30
解得:![]() 或
或![]() .
.
答:甲出发![]() 小时或
小时或![]() 小时两人相距30千米.
小时两人相距30千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成推理过程
(1)如图,已知∠1=∠2,∠B=∠C,求证:AB∥CD.
证明∵∠1=∠2(已知),
且∠1=∠CGD( )
∴∠2=∠CGD( ),
∴CE∥BF( ),
∴∠C=∠BFD( )
又∵∠B=∠C(已知),
∴∠BFD=∠B( ),
∴AB∥CD( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】公司投资750万元,成功研制出一种市场需求量较大的产品,并再投入资金1750万元进行相关生产设备的改进.已知生产过程中,每件产品的成本为60元.在销售过程中发现,当销售单价定为120元时,年销售量为24万件;销售单价每增加10元,年销售量将减少1万件.设销售单价为x(元)(x>120),年销售量为y(万件),第一年年获利(年获利=年销售额﹣生产成本)为z(万元).
(1)求出y与x之间,z与x之间的函数关系式;
(2)该公司能否在第一年收回投资. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F,

DE与AB相交于点E.
(1)求证:ABAF=CBCD;
(2)已知AB=15cm,BC=9cm,P是线段DE上的动点.设DP=x cm,梯形BCDP的面积为y .
.
①求y关于x的函数关系式.
②y是否存在最大值?若有求出这个最大值,若不存在请说明理由. -
科目: 来源: 题型:
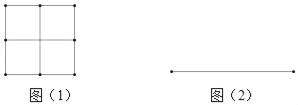
查看答案和解析>>【题目】(一)问题提出:如何把n个边长为1的正方形,剪拼成一个大正方形?
(二)解决方法
探究一:若n是完全平方数,我们不用剪切小正方形,可直接将小正方形拼成一个大正方形,如图(1),用四个边长为1的小正方形可以拼成一个大正方形.
问题1:请用9个边长为1的小正方形在图(2)的位置拼成一个大正方形.
探究二:若n=2,5,10,13等这些数,都可以用两个正整数的平方和来表示,以n=5为例,用5个边长为1的小正方形剪拼成一个大正方形.
(1)计算:拼成的大正方形的面积为5,边长为
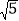 ,可表示成
,可表示成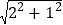 ;
;(2)剪切:如图(3)将5个小正方形按如图所示分成5部分,虚线为剪切线;
(3)拼图:以图(3)中的虚线为边,拼成一个边长为
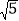 的大正方形,如图(4).
的大正方形,如图(4).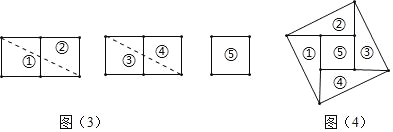
问题2:请仿照上面的研究方式,用13个边长为1的小正方形剪拼成一个大正方形;
(1)计算:拼成的大正方形的面积为____,边长为_____,可表示成____;
(2)剪切:请仿照图(3)的方法,在图(5)的位置画出图形.
(3)拼图:请仿照图(4)的方法,在图(6)的位置出拼成的图.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某射击队有甲、乙两名射手,他们各自射击7次,射中靶的环数记录如下:
甲:8,8,8,9,6,8,9
乙:10,7,8,8,5,10,8
(1)分别求出甲、乙两名射手打靶环数的平均数、众数、中位数;
(2)如果要选择一名成绩比较稳定的射手,代表射击队参加比赛,应如何选择?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=
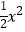 +bx﹣
+bx﹣  的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.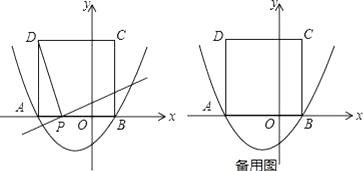
(1)b=;点D的坐标:;
(2)线段AO上是否存在点P(点P不与A、O重合),使得OE的长为1;
(3)在x轴负半轴上是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
相关试题

