Question

【题目】如图，抛物线y= +bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于C（0，﹣3）．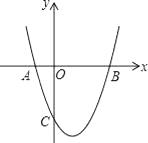

（1）求抛物线的解析式；
（2）D是y轴正半轴上的点，OD=3，在线段BD上任取一点E（不与B，D重合），经过A，B，E三点的圆交直线BC于点F，
①试说明EF是圆的直径；
②判断△AEF的形状，并说明理由．

Answer 1

【答案】
（1）解：∵抛物线y= +bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于C（0，﹣3），

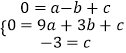∴ ，解得 ，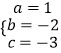

∴抛物线的解析式为y= ﹣2x﹣3；

（2）解：按照题意画出图形，如下图，

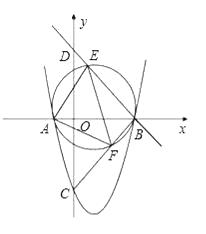
①∵B点坐标（3，0）、C点坐标（0，﹣3），

∴OB=OC=3，

∴△BOC为等腰直角三角形，

∴∠CBO=45°，

又∵D是y轴正半轴上的点，OD=3，

∴△BOD为等腰直接三角形，

∴∠OBD=45°，

∠CBD=∠CBO+∠OBD=45°+45°=90°，

即∠FBE=90°，

∴EF是圆的直径．

②∵∠CBO=∠OBD=45°，∠AFE=∠OBD，∠AEF=∠CBO（在同圆中，同弧所对的圆周角相等），

∴∠AEF=∠AFE=45°，

∴∠FAE=90°，AE=AF，

∴△AEF是等腰直角三角形．

【解析】（1）用待定系数法可以求出抛物线的解析式；
（2）①根据B,C两点的坐标得出OB=OC=3，从而判断出△BOC为等腰直角三角形，根据等腰直角三角形的性质知∠CBO=45°，进而判断出△BOD为等腰直接三角形，从而得出∠OBD=45°，∠FBE=90°，根据圆周角定理得出EF是圆的直径；②根据∠CBO=∠OBD=45°，及在同圆中，同弧所对的圆周角相等得∠AFE=∠OBD，∠AEF=∠CBO，从而得出∠AEF=∠AFE=45°，然后根据三角形内角和及等角对等边得出∠FAE=90°，AE=AF，从而得出结论。
【考点精析】本题主要考查了圆周角定理的相关知识点，需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题．