【题目】小王上周五在股市以收盘价每股![]() 元买进某公司的股票
元买进某公司的股票![]() 股,在接下来的一周交易日内,他记下该股票每日收盘价比前一天的涨跌情况(单位:元):
股,在接下来的一周交易日内,他记下该股票每日收盘价比前一天的涨跌情况(单位:元):
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 |
|
|
|
|
|
(1)星期二收盘时,该股票每股多少元?
(2)本周内,该股票收盘时的最高价、最低价分别是多少?
(3)已知买入股票与卖出股票均需支付成交金额的![]() 的交易费,若小王在本周五以收盘价将全部股票卖出,他的收益情况如何?
的交易费,若小王在本周五以收盘价将全部股票卖出,他的收益情况如何?
参考答案:
【答案】(1)星期二收盘时,该股票每股26.5元;(2)本周内,该股票收盘时的最高价是28元,最低价是26.2元;(3)小王赚了1922元.
【解析】
(1)由题意可知:星期一比上周的星期五涨了2元,星期二比星期一跌了0.5元,则星期二收盘价表示为25+2-0.5,然后计算;
(2)分别求出每天的收盘价格,比较即可得答案;
(3)分别求出买入股票与卖出股票时的金额,用卖出金额减去买入金额即可得答案.
(1)星期二收盘价为25+2-0.5=26.5(元/股).
(2)星期一每股是25+2=27(元);
星期二每股27-0.5=26.5(元);
星期三每股26.5+1.5=28(元);
星期四每股28-1.8=26.2(元);
星期五每股26.2+0.8=27(元)
经过比较可知最高价是28元,最低价是26.2元.
(3)由(2)可知星期五收盘时每股是27元,
则卖出时赚了27×1000×(1-0.15%)=26959.5(元),
买入时花了25×1000×(1+0.15%)=25037.5(元),
所以赚了26959.5-25037.5=1922(元)
答:(1)星期二收盘时,该股票每股26.5元;
(2)本周内,该股票收盘时的最高价是28元,最低价是26.2元;
(3)小王赚了1922元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一些半径相同的小圆按如图所示的规律摆放:
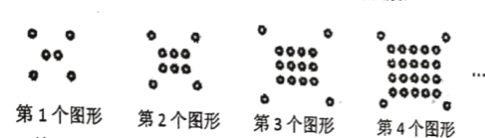
(1)填写下表:
图形序号
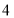
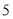
小圆个数
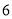
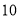
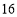
(2)照这样的规律搭下去,摆
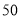 个这样的图形需要 个小圆.
个这样的图形需要 个小圆. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知直线PQ∥MN,点A在直线PQ上,点C、D在直线MN上,连接AC、AD,∠PAC=50°,∠ADC=30°,AE平分∠PAD,CE平分∠ACD,AE与CE相交于E.
(1)求∠AEC的度数;
(2)若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置,此时A1E平分∠AA1D1,CE平分∠ACD1,A1E与CE相交于E,∠PAC=50°,∠A1D1C=30°,求∠A1EC的度数.
(3)若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置,其他条件与(2)相同,求此时∠A1EC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C、D是⊙O上的点,且OC∥BD,AD分别与BC、OC相交于 点E、F.若∠CBD=36°,则下列结论中不正确的是
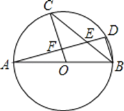
A. ∠AOC=72° B. ∠AEC=72° C. AF=DF D. BD=20F
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,矩形ABCD的位置如图1所示,点A的坐标为(-2,0),点B的坐标为(0,2),点D的坐标为(-3,1).矩形ABCD以每秒1个单位长度的速度沿x轴正方向运动,设运动时间为x(0≤x≤3)秒,第一象限内的图形面积为y,则下列图象中表示y与x的函数关系的图象大致是
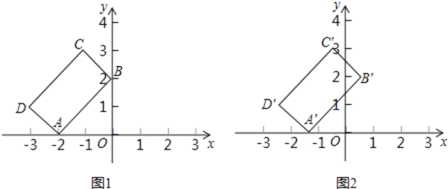
A.
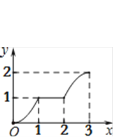 B.
B. 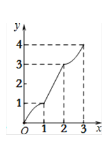 C.
C. 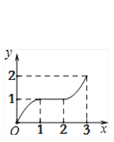 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在圆⊙O中,将弧AB沿弦AB折叠,使弧AB恰好经过圆心O,点P是优弧AMB上一点,则∠APB的度数为_________.
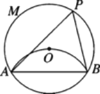
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列四个命题:①无限小数是无理数;②若
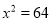 ,则
,则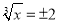 ;③同位角相等;④过一点有且只有一条直线平行于已知直线;⑤平移变换中,对应点的连线线段平行且相等;⑥若一个角的两边与另一个角的两边互相平行,则这两个角一定相等.其中是假命题的个数有
;③同位角相等;④过一点有且只有一条直线平行于已知直线;⑤平移变换中,对应点的连线线段平行且相等;⑥若一个角的两边与另一个角的两边互相平行,则这两个角一定相等.其中是假命题的个数有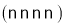
A.5个B.4个C.3个D.2个
相关试题

