【题目】如图1,已知直线PQ∥MN,点A在直线PQ上,点C、D在直线MN上,连接AC、AD,∠PAC=50°,∠ADC=30°,AE平分∠PAD,CE平分∠ACD,AE与CE相交于E.
(1)求∠AEC的度数;
(2)若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置,此时A1E平分∠AA1D1,CE平分∠ACD1,A1E与CE相交于E,∠PAC=50°,∠A1D1C=30°,求∠A1EC的度数.
(3)若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置,其他条件与(2)相同,求此时∠A1EC的度数.

参考答案:
【答案】(1)∠AEC=130°;(2)∠A1EC=130°;(3)∠A1EC=40°.
【解析】
(1)由直线PQ∥MN,∠ADC=∠QAD=30°,可得∠PAD=150°,再求∠PAE=75°,可得∠CAE=25°;由∠PAC=∠ACN,求得∠ECA=25°,故∠AEC=180°﹣25°﹣25°;
(2)先求出∠QA1D1=30°,∠PA1D1=150°,再求出∠PA1E=∠EA1D1=75°,再求出∠CAQ=130°,∠ACN=50°,根据平分线定义得∠ACE=25°,再利用四边形内角和性质可求∠CEA1;
(3)根据平行线性质和角平分线定义可求得∠QA1E=∠2=15°,∠ACE=∠ECN=∠1=25°,再由∠CEA1=∠1+∠2即可求得答案.
(1)如图1所示:

∵直线PQ∥MN,∠ADC=30°,
∴∠ADC=∠QAD=30°,
∴∠PAD=150°,
∵∠PAC=50°,AE平分∠PAD,
∴∠PAE=75°,
∴∠CAE=25°,
可得∠PAC=∠ACN=50°,
∵CE平分∠ACD,
∴∠ECA=25°,
∴∠AEC=180°﹣25°﹣25°=130°;
(2)如图2所示:
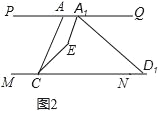
∵∠A1D1C=30°,线段AD沿MN向右平移到A1D1,PQ∥MN,
∴∠QA1D1=30°,
∴∠PA1D1=150°,
∵A1E平分∠AA1D1,
∴∠PA1E=∠EA1D1=75°,
∵∠PAC=50°,PQ∥MN,
∴∠CAQ=130°,∠ACN=50°,
∵CE平分∠ACD1,
∴∠ACE=25°,
∴∠CEA1=360°﹣25°﹣130°﹣75°=130°;
(3)如图3所示:
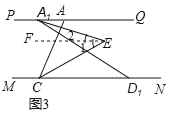
过点E作FE∥PQ,
∵∠A1D1C=30°,线段AD沿MN向左平移到A1D1,PQ∥MN,
∴∠QA1D1=30°,
∵A1E平分∠AA1D1,
∴∠QA1E=∠2=15°,
∵∠PAC=50°,PQ∥MN,
∴∠ACN=50°,
∵CE平分∠ACD1,
∴∠ACE=∠ECN=∠1=25°,
∴∠CEA1=∠1+∠2=15°+25°=40°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)求直线AB的表达式;
(2)若直线AB上有一动点C,且
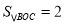 ,求点C的坐标.
,求点C的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种机器可供选择.其中甲型机器每日生产零件106个,乙型机器每日生产零件60个,经调査,购买3台甲型机器和2台乙型机器共需要31万元,购买一台甲型机器比购买一台乙型机器多2万元
(1)求甲、乙两种机器每台各多少万元?
(2)如果工厂期买机器的预算资金不超过34万元,那么你认为该工厂有哪几种购买方案?
(3)在(2)的条件下,如果要求该工厂购进的6台机器的日产量能力不能低于380个,那么为了节约资金.应该选择哪种方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图象与反比例函数
的图象与反比例函数 的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交
的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交 轴、
轴、 轴于点C、D,且S△PBD=4,
轴于点C、D,且S△PBD=4,  .
.
(1)求点D的坐标;
(2)求一次函数与反比例函数的解析式;
(3)根据图象写出当
 时,一次函数的值大于反比例函数的值的
时,一次函数的值大于反比例函数的值的 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知EF⊥AB,CD⊥AB,下列说法:①EF∥CD;②∠B+∠BDG=180°;③若∠1=∠2,则∠1=∠BEF;④若∠ADG=∠B,则∠DGC+∠ACB=180°,其中说法正确的是( )
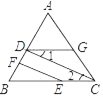
A. ①②B. ③④C. ①②③D. ①③④
-
科目: 来源: 题型:
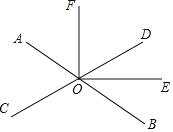
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE平分∠BOD
(1)若∠AOC=60°,求∠BOE的度数;
(2)若OF平分∠AOD,试说明OE⊥OF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.图中描述了他上学的途中离家距离
 (米)与离家时间
(米)与离家时间 (分钟)之间的函数关系.下列说法中正确的个数是( )
(分钟)之间的函数关系.下列说法中正确的个数是( )(1)修车时间为15分钟;
(2)学校离家的距离为4000米;
(3)到达学校时共用时间为20分钟;
(4)自行车发生故障时离家距离为2000米.

A.1个B.2个C.3个D.4个
相关试题

