【题目】“校园安全”受到全社会的广泛关注,东营市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题: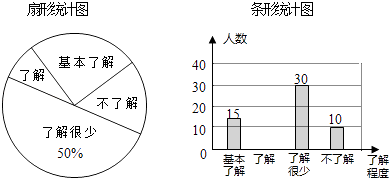
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 ;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
参考答案:
【答案】
(1)60;90°
(2)
解:60﹣15﹣30﹣10=5;
补全条形统计图得:
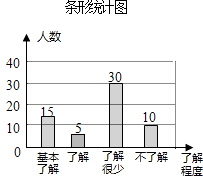
(3)
解:根据题意得:900× ![]() =300(人),
=300(人),
则估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为300人
(4)
解:画树状图得:
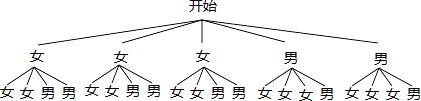
∵共有20种等可能的结果,恰好抽到1个男生和1个女生的有12种情况,
∴恰好抽到1个男生和1个女生的概率为: ![]() =
= ![]()
【解析】解:(1)∵了解很少的有30人,占50%,
∴接受问卷调查的学生共有:30÷50%=60(人);
∴扇形统计图中“基本了解”部分所对应扇形的圆心角为: ![]() ×360°=90°;
×360°=90°;
所以答案是:60,90°;
【考点精析】掌握扇形统计图和条形统计图是解答本题的根本,需要知道能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB,用尺规作∠ABC=90°,作法如下:
小明的作法:(1)分别以A、B为圆心AB长为半径画弧,两弧交于点P;(2)以P为圆心,AB长为半径画弧交AP的延长线于C;连接AC,则∠ABC=90°

(1)请证明∠ABC=90°;
(2)请你用不同的方法,用尺规作∠ABC=90°.
(要求:保留作图痕迹,不写作法,并用2B铅笔把作图痕迹描粗)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中是中心对称图形的是
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|1﹣
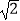 |+(π﹣2014)0﹣2sin45°+(
|+(π﹣2014)0﹣2sin45°+(  )﹣2 .
)﹣2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列解答中,填写适当的理由或数学式:

(1)∵ ∠ABD=∠CDB, ( 已知 )
∴ ∥ . ( )
(2)∵ ∠ADC+∠DCB=180°, ( 已知 )
∴ ∥ . ( )
(3)∵ AD∥BE, ( 已知 )
∴ ∠DCE=∠ . ( )
(4)∵ ∥ , ( 已知 )
∴ ∠BAE=∠CFE. ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明骑车从家出发,先向东骑行1km到达A村,继续向东骑行4km到达B村,然后向西骑行8km到达C村,最后回到家.
(1) 以快递公司为原点,以向东方向为正方向,用1 cm表示1 km,画出数轴,并在数轴上表示出A、B、C三个店的位置;
(2) C店离A店有多远?
(3) 快递员一共骑行了多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】快车和慢车同时从甲、乙两地出发开往乙地和甲地,匀速行驶,快车到达乙地后休息一个小时按原速返回,慢车在快车前一个小时到达甲地.如图表示慢车行驶过程中离甲地的路程y(km)与出发时间x(h)的函数图象,请结合图中的信息,解答下列问题:

(1)甲、乙两地的距离为 km,慢车的速度为 km/h,快车的速度为 km/h;
(2)在图①中画出快车离甲地的路程y(km)与出发时间x(h)的函数图象(坐标轴标注相关数值);
(3)求出发多长时间,两车相距150km.
相关试题

