【题目】已知线段AB,用尺规作∠ABC=90°,作法如下:
小明的作法:(1)分别以A、B为圆心AB长为半径画弧,两弧交于点P;(2)以P为圆心,AB长为半径画弧交AP的延长线于C;连接AC,则∠ABC=90° |
|
(1)请证明∠ABC=90°;
(2)请你用不同的方法,用尺规作∠ABC=90°.
(要求:保留作图痕迹,不写作法,并用2B铅笔把作图痕迹描粗)
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)想办法怎么∠A=60°,∠C=30°即可解决问题;
(2)以B为圆心任意长为半径画弧交直线AB于E、F,分别以E、F为圆心大于![]() EF长为半径画弧,两弧交于点P,作射线BP,在射线BP上任意取一点C,∠ABC即为所求.
EF长为半径画弧,两弧交于点P,作射线BP,在射线BP上任意取一点C,∠ABC即为所求.
(1)证明:如图连接PB.
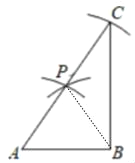
∵PA=PB=AB,
∴△PAB是等边三角形,
∴∠APB=∠A=60°,
∵PC=PB,
∴∠C=∠PBC,
∵∠APB=∠C+∠PBC,
∴∠C=30°,
∴∠A+∠C=90°,
∴∠ABC=90°.
(2)如图,∠ABC=90°即为所求.
-
科目: 来源: 题型:
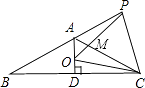
查看答案和解析>>【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP , 其中正确的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E,H,G,N在同一直线上,△EFG≌△NMH,∠F和∠M是对应角.在△EFG中,FG是最长边.在△NMH中,MH是最长边.已知EF=2.1 cm,EH=1.1 cm,HN=3.3 cm.
(1)写出其他对应边及对应角;
(2)求线段MN及线段HG的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=
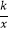 经过正方形AOBC对角线的交点,半径为(6﹣3
经过正方形AOBC对角线的交点,半径为(6﹣3 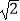 )的圆内切于△ABC,则k的值为 .
)的圆内切于△ABC,则k的值为 . 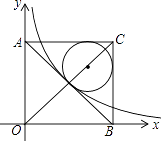
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中是中心对称图形的是
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|1﹣
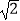 |+(π﹣2014)0﹣2sin45°+(
|+(π﹣2014)0﹣2sin45°+(  )﹣2 .
)﹣2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】“校园安全”受到全社会的广泛关注,东营市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
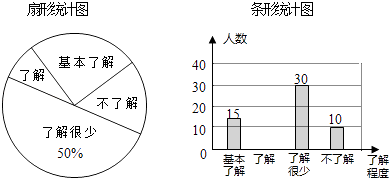
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 ;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
相关试题


