【题目】(几何背景)如图1,AD为锐角△ABC的高,垂足为D.求证:AB2﹣AC2=BD2﹣CD2
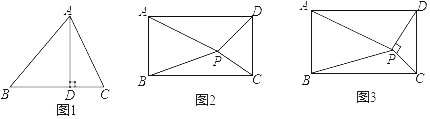
(知识迁移)如图2,矩形ABCD内任意一点P,连接PA、PB、PC、PD,请写出PA、PB、PC、PD之间的数量关系,并说明理由.
(拓展应用)如图3,矩形ABCD内一点P,PC⊥PD,若PA=a,PB=b,AB=c,且a、b、c满足a2﹣b2=![]() c2,则
c2,则![]() 的值为 (请直接写出结果)
的值为 (请直接写出结果)
参考答案:
【答案】【几何背景】:详见解析;【知识迁移】:详见解析;【拓展应用】:![]()
【解析】
几何背景:由 Rt△ABD中,AD2=AB2﹣BD2,Rt△ACD中,AD2=AC2﹣CD2,则结论可证.
知识迁移:过P点作PE⊥AD,延长EP交BC于F,可证四边形ABFE,四边形DCFE是矩形.根据上面的结论求得PA、PB、PC、PD之间的数量关系.
拓展应用:根据勾股定理可列方程组,可求PD=![]() c,PC=
c,PC=![]() c即可得
c即可得![]() .
.
解:几何背景:在Rt△ABD中,AD2=AB2﹣BD2
Rt△ACD中,AD2=AC2﹣CD2,
∴AB2﹣BD2=AC2﹣CD2,
∴AB2﹣AC2=BD2﹣CD2.
知识迁移:BP2﹣PC2 =BF2﹣CF2.
如 图:
过P点作PE⊥AD,延长EP交BC于F
∴四边形ABCD是矩形
∴AD∥BC∠BAD=∠ADC=∠DCB=∠ABC=90°
又∵PE⊥AD
∴PF⊥BC
∵PE是△APD的高
∴PA2﹣PD2=AE2﹣DE2.
∵PF是△PBC的高
∴BP2﹣PC2 =BF2﹣CF2.
∵∠BAD=∠ADC=∠DCB=∠ABC=90°,PE⊥AD,PF⊥BC
∴四边形ABFE,四边形DCFE是矩形
∴AE=BF,CF=DE
∴PA2﹣PD2=BP2﹣PC2.
拓展应用:∵PA2﹣PD2=BP2﹣PC2.
∴PA2﹣PB2=![]() c2.
c2.
∴PD2﹣PC2=![]() c2.
c2.
且PD2+PC2=c2.
∴PD=![]() c,PC=
c,PC=![]() c
c
∴![]() ,
,
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料:
点A、B在数轴上分别表示实数a,b,A,B两点之间的距离表示为|AB|
当A、B两点中有一点在原点时,设点A在原点,如图①|AB|=|OB|=|b|=|a﹣b|
当A、B两点都不在原点时,

(1)如图②,点A,B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
(2)如图③,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|
(3)如图④,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=|a﹣b|
综上所述,数轴上A、B两点之间的距离|AB|=|a﹣b|
请用上面的知识解答下面的问题:
(1)数轴上表示﹣2和﹣4的两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 .
(2)数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2,那么x为 .
(3)当|x+1|+|x﹣2|=5时的整数x的值 .
(4)当|x+1|+|x﹣2|取最小值时,相应的x的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式:
①(2a+b)(m+n);②2a(m+n)+b(m+n);③m(2a+b)+n(2a+b);④2am+2an+bm+bn,你认为其中正确的有( )

A. ①② B. ③④ C. ①②③ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】“低碳生活,绿色出行”,共享单车已经成了很多人出行的主要选择,今年1月份,“摩拜”共享单车又向长沙河西新投放共享单车640辆.
(1)若1月份到3月份新投放单车数量的月平均增长率相同,3月份新投放共享单车1000辆.求月平均增长率。
(2)考虑到共享单车市场竞争激烈,摩拜公司准备用不超过60000元的资金再购进A,B两种规格的自行车100辆,且A型车不超过60辆。已知A型的进价为500元/辆,B型车进价为700元/辆,设购进A型车m辆,求出m的取值范围。
(3)已知A型车每月产生的利润是100元/辆,B型车每月产生的利润是90元/辆,在(2)的条件下,求公司每月的最大利润。
-
科目: 来源: 题型:
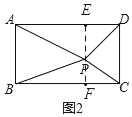
查看答案和解析>>【题目】如图,正方形ABCD与正方形BFGE中,点E在边AB上,若AE=a,BE=b,(其中a>2b).
(1)请用含有a,b的代数式表示图中阴影部分的面积;
(2)当a=5cm,b=3cm时,求阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AO为Rt△ABC的角平分线,∠ACB=90°,
 ,以O为圆心,OC 为半径的圆分别交AO,BC于点D,E,连接ED并延长交AC于点F.
,以O为圆心,OC 为半径的圆分别交AO,BC于点D,E,连接ED并延长交AC于点F.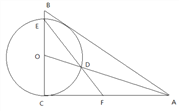
(1)求证:AB是⊙O的切线;
(2)求
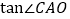 的值。
的值。(3)若⊙O的半径为4,求
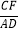 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个三位数,十位数字是
 ,百位数字是十位数字的2倍,个位数字比十位数字小2.
,百位数字是十位数字的2倍,个位数字比十位数字小2.(1)试用代数式表示出这个三位数.
(2)试写出所有符合条件的三位数.
相关试题

