【题目】如图,已知AO为Rt△ABC的角平分线,∠ACB=90°,![]() ,以O为圆心,OC 为半径的圆分别交AO,BC于点D,E,连接ED并延长交AC于点F.
,以O为圆心,OC 为半径的圆分别交AO,BC于点D,E,连接ED并延长交AC于点F.
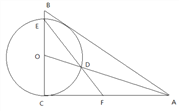
(1)求证:AB是⊙O的切线;
(2)求![]() 的值。
的值。
(3)若⊙O的半径为4,求![]() 的值.
的值.
参考答案:
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】分析:(1)作垂直,证半径,先根据AAS证明△OGA≌△OCA,可得OC=OG,可知OG为为⊙O的半径,可得结论;(2)设AC=4x,BC=3x,则AB=5x,根据等角的三角函数可得tan∠CAO=tan∠GAO=![]() ;(3)先根据勾股定理求得AO=
;(3)先根据勾股定理求得AO=![]() ,则求得AD=OA-OD=
,则求得AD=OA-OD=![]() .证明△DFA∽△CDA,列比例式DA:AC=AF:AD,代入可得AF的长,代入可得结论.
.证明△DFA∽△CDA,列比例式DA:AC=AF:AD,代入可得AF的长,代入可得结论.
详解:(1)证明:作OG⊥AB于点G.
∵∠ACB=∠OGA=90°,∠GAO=∠CAO,AO=AO,
∴△OGA≌△OCA,
∴OC=OG,
∵OC为⊙O的半径,
∴AB是⊙O的切线;
(2)解:设AC=4x,BC=3x,则AB=5x,
由切线长定理知,AC=AG=4x,故BG=x.
∵tan∠B=OG:BG=AC:BC=4:3,
∴OG=![]() ,
,
∴tan∠CAO=tan∠GAO=![]() =
=![]() =
=![]() ;
;
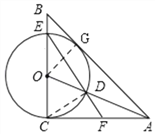
(3)解:由(2)可知 在Rt△OCA中,AO=![]()
∴AD=OA﹣OD=![]()
连接CD,则∠DCF+∠ECD=∠ECD+∠CEF,
∴∠DCF=∠CEF,
又∠CEF=∠EDO=∠FDA,
∴∠DCF=∠ADF,又∠FAD=∠DAC,
∴△DFA∽△CDA,
∴DA:AC=AF:AD,
即![]() :12=AF:
:12=AF:![]()
∴AF=![]() ,CF=12-
,CF=12-![]() =
=![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】“低碳生活,绿色出行”,共享单车已经成了很多人出行的主要选择,今年1月份,“摩拜”共享单车又向长沙河西新投放共享单车640辆.
(1)若1月份到3月份新投放单车数量的月平均增长率相同,3月份新投放共享单车1000辆.求月平均增长率。
(2)考虑到共享单车市场竞争激烈,摩拜公司准备用不超过60000元的资金再购进A,B两种规格的自行车100辆,且A型车不超过60辆。已知A型的进价为500元/辆,B型车进价为700元/辆,设购进A型车m辆,求出m的取值范围。
(3)已知A型车每月产生的利润是100元/辆,B型车每月产生的利润是90元/辆,在(2)的条件下,求公司每月的最大利润。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(几何背景)如图1,AD为锐角△ABC的高,垂足为D.求证:AB2﹣AC2=BD2﹣CD2
(知识迁移)如图2,矩形ABCD内任意一点P,连接PA、PB、PC、PD,请写出PA、PB、PC、PD之间的数量关系,并说明理由.
(拓展应用)如图3,矩形ABCD内一点P,PC⊥PD,若PA=a,PB=b,AB=c,且a、b、c满足a2﹣b2=
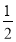 c2,则
c2,则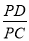 的值为 (请直接写出结果)
的值为 (请直接写出结果)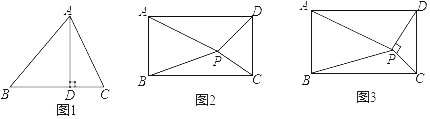
-
科目: 来源: 题型:
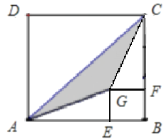
查看答案和解析>>【题目】如图,正方形ABCD与正方形BFGE中,点E在边AB上,若AE=a,BE=b,(其中a>2b).
(1)请用含有a,b的代数式表示图中阴影部分的面积;
(2)当a=5cm,b=3cm时,求阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个三位数,十位数字是
 ,百位数字是十位数字的2倍,个位数字比十位数字小2.
,百位数字是十位数字的2倍,个位数字比十位数字小2.(1)试用代数式表示出这个三位数.
(2)试写出所有符合条件的三位数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题
阅读材料:
两个两位数相乘,如果这两个因数的十位数字相同,个位数字的和是10,该类乘法的速算方法是:将一个因数的十位数字与另一个因数的十位数字加1的和相乘,所得的积作为计算结果的前两位,将两个因数的个位数字之积作为计算结果的后两位(数位不足两位,用0补齐)。
比如
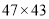 ,它们乘积的前两位是
,它们乘积的前两位是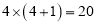 ,它们乘积的后两位是
,它们乘积的后两位是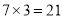 ,所以
,所以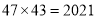 ;
;再如
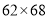 ,它们乘积的前两位是
,它们乘积的前两位是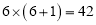 ,它们乘积的后两位是
,它们乘积的后两位是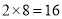 ,所以
,所以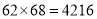 ;
;又如
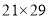 ,
,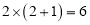 ,不足两位,就将6写在百位:
,不足两位,就将6写在百位: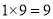 ,不足两位,就将9写在个位,十位上写0,所以
,不足两位,就将9写在个位,十位上写0,所以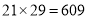
该速算方法可以用我们所学的整式乘法与分解因式的知识说明其合理性;
设其中一个因数的十位数字为
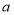 ,个位数字是
,个位数字是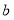 ,(
,(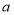 、
、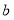 表示1~9的整数),则该数可表示为
表示1~9的整数),则该数可表示为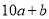 ,另一因数可表示为
,另一因数可表示为 .
.两数相乘可得:
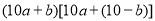
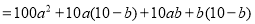
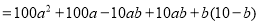
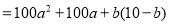
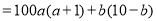 .
.(注:其中
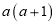 表示计算结果的前两位,
表示计算结果的前两位, 表示计算结果的后两位。)
表示计算结果的后两位。)问题:
两个两位数相乘,如果其中一个因数的十位数字与个位数字相同,另一因数的十位数字与个位数字之和是10.
如
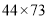 、
、 、
、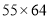 等.
等.(1)探索该类乘法的速算方法,请以
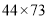 为例写出你的计算步骤;
为例写出你的计算步骤;(2)设十位数字与个位数字相同的因数的十位数字是
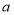 ,则该数可以表示为___________.
,则该数可以表示为___________.设另一个因数的十位数字是
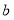 ,则该数可以表示为___________.(
,则该数可以表示为___________.(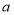 、
、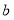 表示1~9的正整数)
表示1~9的正整数)(3)请针对问题(1)(2)中的计算,模仿阅读材料中所用的方法写出如:
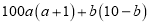 的运算式:____________________
的运算式:____________________ -
科目: 来源: 题型:
查看答案和解析>>【题目】某市“艺术节”期间,小明、小亮都想去观看茶艺表演,但是只有一张茶艺表演 门票,他们决定采用抽卡片的办法确定谁去.规则如下:
将正面分别标有数字 1、2、3、4 的四张卡片(除数字外其余都相同)洗匀后,背面朝上 放置在桌面上,随机抽出一张记下数字后放回;重新洗匀后背面朝上放置在桌面上, 再随机抽出一张记下数字.如果两个数字之和为奇数,则小明去;如果两个数字之和 为偶数,则小亮去.
(1)请用列表或画树状图的方法表示抽出的两张卡片上的数字之和的所有可能出现 的结果;
(2)你认为这个规则公平吗?请说明理由.
相关试题

