搜索
【题目】已知一个三位数，十位数字是
，百位数字是十位数字的2倍，个位数字比十位数字小2．
（1）试用代数式表示出这个三位数．
（2）试写出所有符合条件的三位数．
参考答案：
【答案】(1) 
．(2) 842，631，420
【解析】
（1）由于这个三位数的十位数字是a，个位数字比十位数字小2，则个位数字为：a-2，百位数字是十位数字的2倍，则百位数字为：2a，再列代数式表示出这个三位数即可；
（2）根据三位数的最大取值，结合代数式求得答案即可．
解：（1）由题意得：这个三位数的十位数字是
，个位数字是
，百位数字是
，
则这个三位数为：
．
（2）由是三位数，则可以为4、3、2、1，
所以这个三位数可以是：842，631，420，219（不合题意），
符合条件的有842，631，420三个数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（几何背景）如图1，AD为锐角△ABC的高，垂足为D．求证：AB2﹣AC2＝BD2﹣CD2
（知识迁移）如图2，矩形ABCD内任意一点P，连接PA、PB、PC、PD，请写出PA、PB、PC、PD之间的数量关系，并说明理由．
（拓展应用）如图3，矩形ABCD内一点P，PC⊥PD，若PA＝a，PB＝b，AB＝c，且a、b、c满足a2﹣b2＝
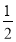c2，则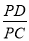
的值为 （请直接写出结果）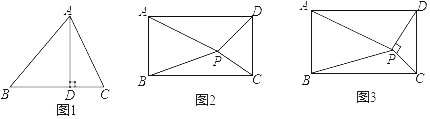
-
科目： 来源： 题型：
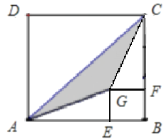
查看答案和解析>>【题目】如图，正方形ABCD与正方形BFGE中，点E在边AB上，若AE=a，BE=b，（其中a＞2b）．
（1）请用含有a，b的代数式表示图中阴影部分的面积；
（2）当a=5cm，b=3cm时，求阴影部分的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知AO为Rt△ABC的角平分线，∠ACB=90°，
，以O为圆心，OC 为半径的圆分别交AO，BC于点D，E，连接ED并延长交AC于点F．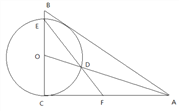
（1）求证：AB是⊙O的切线；
（2）求
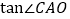的值。（3）若⊙O的半径为4，求
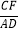的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解题
阅读材料：
两个两位数相乘，如果这两个因数的十位数字相同，个位数字的和是10，该类乘法的速算方法是：将一个因数的十位数字与另一个因数的十位数字加1的和相乘，所得的积作为计算结果的前两位，将两个因数的个位数字之积作为计算结果的后两位（数位不足两位，用0补齐）。
比如
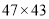，它们乘积的前两位是
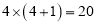，它们乘积的后两位是
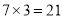，所以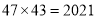
；再如
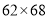，它们乘积的前两位是
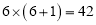，它们乘积的后两位是
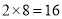，所以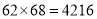
；又如
，
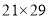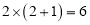，不足两位，就将6写在百位：
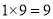，不足两位，就将9写在个位，十位上写0，所以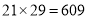
该速算方法可以用我们所学的整式乘法与分解因式的知识说明其合理性；
设其中一个因数的十位数字为
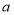，个位数字是
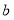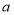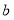，（、表示1~9的整数），则该数可表示为
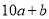，另一因数可表示为
．两数相乘可得：
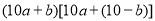
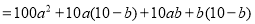
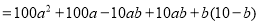
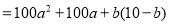
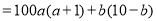.（注：其中
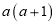表示计算结果的前两位，
表示计算结果的后两位。）问题：
两个两位数相乘，如果其中一个因数的十位数字与个位数字相同，另一因数的十位数字与个位数字之和是10．
如
、
、
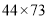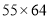等．（1）探索该类乘法的速算方法，请以
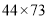为例写出你的计算步骤；（2）设十位数字与个位数字相同的因数的十位数字是
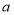，则该数可以表示为___________．设另一个因数的十位数字是
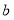，则该数可以表示为___________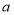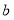．（、表示1~9的正整数）（3）请针对问题（1）（2）中的计算，模仿阅读材料中所用的方法写出如：
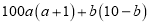的运算式：____________________ -
科目： 来源： 题型：
查看答案和解析>>【题目】某市“艺术节”期间，小明、小亮都想去观看茶艺表演，但是只有一张茶艺表演 门票，他们决定采用抽卡片的办法确定谁去.规则如下：
将正面分别标有数字 1、2、3、4 的四张卡片（除数字外其余都相同）洗匀后，背面朝上 放置在桌面上，随机抽出一张记下数字后放回；重新洗匀后背面朝上放置在桌面上， 再随机抽出一张记下数字.如果两个数字之和为奇数，则小明去；如果两个数字之和 为偶数，则小亮去.
（1）请用列表或画树状图的方法表示抽出的两张卡片上的数字之和的所有可能出现 的结果；
（2）你认为这个规则公平吗？请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，点D，E，F分别是AB，BC，AC的中点，连接DE，EF，DF，则下列说法不正确的是（ ）
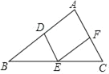
A. S△DEF＝
S△ABCB. △DEF≌△FAD≌△EDB≌△CFE
C. 四边形ADEF，四边形DBEF，四边形DECF都是平行四边形
D. 四边形ADEF的周长＝四边形DBEF的周长＝四边形DECF的周长
相关试题
