【题目】甲、乙两地相距210千米,一辆货车将货物由甲地运至乙地,卸载后返回甲地.若货车距乙地的距离y(千米)与时间t(时)的关系如图所示,根据所提供的信息,回答下列问题:
(1)货车在乙地卸货停留了多长时间?
(2)货车往返速度,哪个快?返回速度是多少?

参考答案:
【答案】(1)1小时;(2)返回速度快,70千米/时.
【解析】
(1)根据函数图象通过是信息可知,4.5-3.5=1,由此得出货车在乙地卸货停留的时间;
(2)比较货车往返所需的时间,即可得出货车往返速度的大小关系,根据路程除以时间即可求得速度.
解:(1)∵4.5-3.5=1(小时),∴货车在乙地卸货停留了1小时.
(2)∵7.5-4.5=3<3.5,∴货车返回速度快.
∵210÷3=70(千米/时),
∴返回速度是70千米/时.
故答案为:(1)1小时;(2)返回速度快,70千米/时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,李老师出示了如下框中的题目.

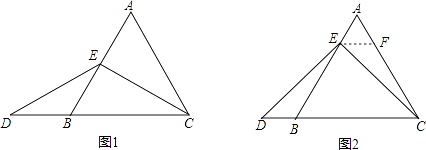
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:AEDB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AEDB(填“>”,“<”或“=”).理由如下:
如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,用长为20的铁丝焊接成一个长方形,设长方形的一边为x,面积为y,随着x的变化,y的值也随之变化.
(1)写出y与x之间的关系式,并指出在这个变化中,哪个是自变量?哪个是因变量?

(2)用表格表示当x从1变化到9时(每次增加1),y的相应值;
x
1
2
3
4
5
6
7
8
9
y
(3)当x为何值时,y的值最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】温度的变化是人们在生活中经常谈论的话题,请你根据下图回答下列问题:
(1)上午9时的温度是多少?这一天的最高温度是多少?
(2)这一天的温差是多少?从最低温度到最高温度经过了多长时间?
(3)在什么时间范围内温度在下降?图中的A点表示的是什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在如下三个函数图象中,有两个函数图象能近似地刻画如下
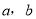 两个情境:
两个情境:
情境
 :小芳离开家不久,发现把作业本忘在家里,于是返回家里找到了作业本再去学校;
:小芳离开家不久,发现把作业本忘在家里,于是返回家里找到了作业本再去学校;情境
 :小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.
:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.(1)情境
 ,
,  所对应的函数图象分别为 , (填写序号).
所对应的函数图象分别为 , (填写序号).(2)请你为剩下的函数图象写出一个适合的情境.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣
 (x﹣1)2+3与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.
(x﹣1)2+3与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.
(1)如图1.求点A的坐标及线段OC的长;
(2)点P在抛物线上,直线PQ∥BC交x轴于点Q,连接BQ.
①若含45°角的直角三角板如图2所示放置.其中,一个顶点与点C重合,直角顶点D在BQ上,另一个顶点E在PQ上.求直线BQ的函数解析式;
②若含30°角的直角三角板一个顶点与点C重合,直角顶点D在直线BQ上,另一个顶点E在PQ上,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】衢州市新农村建设推动了农村住宅旧貌变新颜,如图为一农村民居侧面截图,屋坡AF、AG分别架在墙体的点B、点C处,且AB=AC,侧面四边形BDEC为矩形.若测得∠FAG=110°,则∠FBD=( )
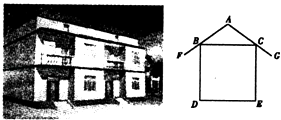
A.35°
B.40°
C.55°
D.70°
相关试题

